Introduction
This is the post of 2020, so happy new year to you all !
I’m a huge fan of LLVM since 11 years ago when I started playing with it to JIT data structures such as AVLs, then later to JIT restricted AST trees and to JIT native code from TensorFlow graphs. Since then, LLVM evolved into one of the most important compiler framework ecosystem and is used nowadays by a lot of important open-source projects.
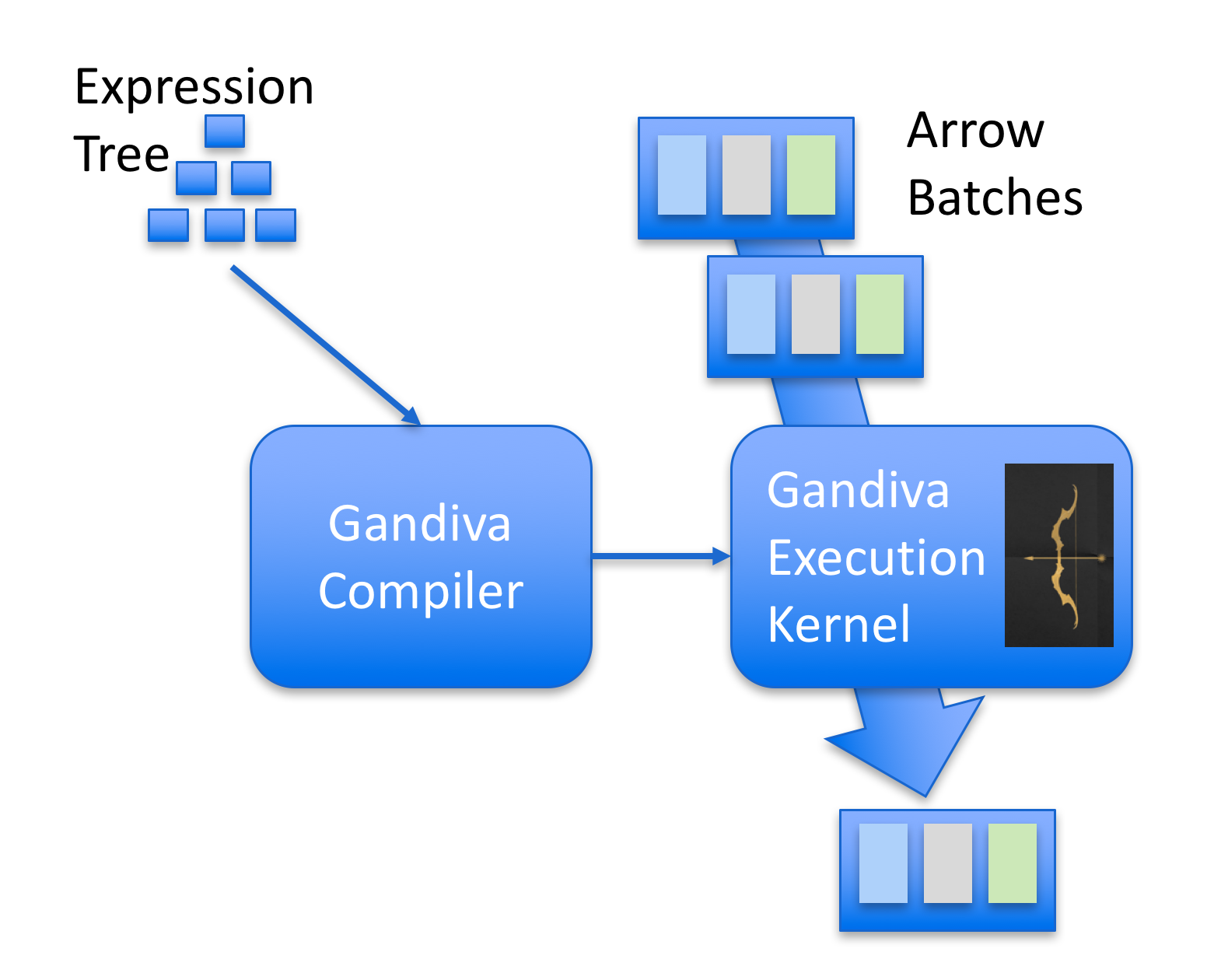
One cool project that I recently became aware of is Gandiva. Gandiva was developed by Dremio and then later donated to Apache Arrow (kudos to Dremio team for that). The main idea of Gandiva is that it provides a compiler to generate LLVM IR that can operate on batches of Apache Arrow. Gandiva was written in C++ and comes with a lot of different functions implemented to build an expression tree that can be JIT’ed using LLVM. One nice feature of this design is that it can use LLVM to automatically optimize complex expressions, add native target platform vectorization such as AVX while operating on Arrow batches and execute native code to evaluate the expressions.
The image below gives an overview of Gandiva:
In this post I’ll build a very simple expression parser supporting a limited set of operations that I will use to filter a Pandas DataFrame.
Building simple expression with Gandiva
In this section I’ll show how to create a simple expression manually using tree builder from Gandiva.
Using Gandiva Python bindings to JIT and expression
Before building our parser and expression builder for expressions, let’s manually build a simple expression with Gandiva. First, we will create a simple Pandas DataFrame with numbers from 0.0 to 9.0:
import pandas as pd
import pyarrow as pa
import pyarrow.gandiva as gandiva
# Create a simple Pandas DataFrame
df = pd.DataFrame({"x": [1.0 * i for i in range(10)]})
table = pa.Table.from_pandas(df)
schema = pa.Schema.from_pandas(df)
We converted the DataFrame to an Arrow Table, it is important to note that in this case it was a zero-copy operation, Arrow isn’t copying data from Pandas and duplicating the DataFrame. Later we get the schemafrom the table, that contains column types and other metadata.
After that, we want to use Gandiva to build the following expression to filter the data:
(x > 2.0) and (x < 6.0)
This expression will be built using nodes from Gandiva:
builder = gandiva.TreeExprBuilder()
# Reference the column "x"
node_x = builder.make_field(table.schema.field("x"))
# Make two literals: 2.0 and 6.0
two = builder.make_literal(2.0, pa.float64())
six = builder.make_literal(6.0, pa.float64())
# Create a function for "x > 2.0"
gt_five_node = builder.make_function("greater_than",
[node_x, two],
pa.bool_())
# Create a function for "x < 6.0"
lt_ten_node = builder.make_function("less_than",
[node_x, six],
pa.bool_())
# Create an "and" node, for "(x > 2.0) and (x < 6.0)"
and_node = builder.make_and([gt_five_node, lt_ten_node])
# Make the expression a condition and create a filter
condition = builder.make_condition(and_node)
filter_ = gandiva.make_filter(table.schema, condition)
This code now looks a little more complex but it is easy to understand. We are basically creating the nodes of a tree that will represent the expression we showed earlier. Here is a graphical representation of what it looks like:
Inspecting the generated LLVM IR
Unfortunately, haven’t found a way to dump the LLVM IR that was generated using the Arrow’s Python bindings, however, we can just use the C++ API to build the same tree and then look at the generated LLVM IR:
auto field_x = field("x", float32());
auto schema = arrow::schema({field_x});
auto node_x = TreeExprBuilder::MakeField(field_x);
auto two = TreeExprBuilder::MakeLiteral((float_t)2.0);
auto six = TreeExprBuilder::MakeLiteral((float_t)6.0);
auto gt_five_node = TreeExprBuilder::MakeFunction("greater_than",
{node_x, two}, arrow::boolean());
auto lt_ten_node = TreeExprBuilder::MakeFunction("less_than",
{node_x, six}, arrow::boolean());
auto and_node = TreeExprBuilder::MakeAnd({gt_five_node, lt_ten_node});
auto condition = TreeExprBuilder::MakeCondition(and_node);
std::shared_ptr<Filter> filter;
auto status = Filter::Make(schema, condition, TestConfiguration(), &filter);
The code above is the same as the Python code, but using the C++ Gandiva API. Now that we built the tree in C++, we can get the LLVM Module and dump the IR code for it. The generated IR is full of boilerplate code and the JIT’ed functions from the Gandiva registry, however the important parts are show below:
; Function Attrs: alwaysinline norecurse nounwind readnone ssp uwtable
define internal zeroext i1 @less_than_float32_float32(float, float) local_unnamed_addr #0 {
%3 = fcmp olt float %0, %1
ret i1 %3
}
; Function Attrs: alwaysinline norecurse nounwind readnone ssp uwtable
define internal zeroext i1 @greater_than_float32_float32(float, float) local_unnamed_addr #0 {
%3 = fcmp ogt float %0, %1
ret i1 %3
}
(...)
%x = load float, float* %11
%greater_than_float32_float32 = call i1 @greater_than_float32_float32(float %x, float 2.000000e+00)
(...)
%x11 = load float, float* %15
%less_than_float32_float32 = call i1 @less_than_float32_float32(float %x11, float 6.000000e+00)
As you can see, on the IR we can see the call to the functions less_than_float32_float_32 and greater_than_float32_float32that are the (in this case very simple) Gandiva functions to do float comparisons. Note the specialization of the function by looking at the function name prefix.
What is quite interesting is that LLVM will apply all optimizations in this code and it will generate efficient native code for the target platform while Godiva and LLVM will take care of making sure that memory alignment will be correct for extensions such as AVX to be used for vectorization.
This IR code I showed isn’t actually the one that is executed, but the optimized one. And in the optimized one we can see that LLVM inlined the functions, as shown in a part of the optimized code below:
%x.us = load float, float* %10, align 4 %11 = fcmp ogt float %x.us, 2.000000e+00 %12 = fcmp olt float %x.us, 6.000000e+00 %not.or.cond = and i1 %12, %11
You can see that the expression is now much simpler after optimization as LLVM applied its powerful optimizations and inlined a lot of Gandiva funcions.
Building a Pandas filter expression JIT with Gandiva
Now we want to be able to implement something similar as the Pandas’ DataFrame.query()function using Gandiva. The first problem we will face is that we need to parse a string such as (x > 2.0) and (x < 6.0), later we will have to build the Gandiva expression tree using the tree builder from Gandiva and then evaluate that expression on arrow data.
Now, instead of implementing a full parsing of the expression string, I’ll use the Python AST module to parse valid Python code and build an Abstract Syntax Tree (AST) of that expression, that I’ll be later using to emit the Gandiva/LLVM nodes.
The heavy work of parsing the string will be delegated to Python AST module and our work will be mostly walking on this tree and emitting the Gandiva nodes based on that syntax tree. The code for visiting the nodes of this Python AST tree and emitting Gandiva nodes is shown below:
class LLVMGandivaVisitor(ast.NodeVisitor):
def __init__(self, df_table):
self.table = df_table
self.builder = gandiva.TreeExprBuilder()
self.columns = {f.name: self.builder.make_field(f)
for f in self.table.schema}
self.compare_ops = {
"Gt": "greater_than",
"Lt": "less_than",
}
self.bin_ops = {
"BitAnd": self.builder.make_and,
"BitOr": self.builder.make_or,
}
def visit_Module(self, node):
return self.visit(node.body[0])
def visit_BinOp(self, node):
left = self.visit(node.left)
right = self.visit(node.right)
op_name = node.op.__class__.__name__
gandiva_bin_op = self.bin_ops[op_name]
return gandiva_bin_op([left, right])
def visit_Compare(self, node):
op = node.ops[0]
op_name = op.__class__.__name__
gandiva_comp_op = self.compare_ops[op_name]
comparators = self.visit(node.comparators[0])
left = self.visit(node.left)
return self.builder.make_function(gandiva_comp_op,
[left, comparators], pa.bool_())
def visit_Num(self, node):
return self.builder.make_literal(node.n, pa.float64())
def visit_Expr(self, node):
return self.visit(node.value)
def visit_Name(self, node):
return self.columns[node.id]
def generic_visit(self, node):
return node
def evaluate_filter(self, llvm_mod):
condition = self.builder.make_condition(llvm_mod)
filter_ = gandiva.make_filter(self.table.schema, condition)
result = filter_.evaluate(self.table.to_batches()[0],
pa.default_memory_pool())
arr = result.to_array()
pd_result = arr.to_numpy()
return pd_result
@staticmethod
def gandiva_query(df, query):
df_table = pa.Table.from_pandas(df)
llvm_gandiva_visitor = LLVMGandivaVisitor(df_table)
mod_f = ast.parse(query)
llvm_mod = llvm_gandiva_visitor.visit(mod_f)
results = llvm_gandiva_visitor.evaluate_filter(llvm_mod)
return results
As you can see, the code is pretty straightforward as I’m not supporting every possible Python expressions but a minor subset of it. What we do in this class is basically a conversion of the Python AST nodes such as Comparators and BinOps (binary operations) to the Gandiva nodes. I’m also changing the semantics of the & and the | operators to represent AND and OR respectively, such as in Pandas query()function.
Register as a Pandas extension
The next step is to create a simple Pandas extension using the gandiva_query() method that we created:
@pd.api.extensions.register_dataframe_accessor("gandiva")
class GandivaAcessor:
def __init__(self, pandas_obj):
self.pandas_obj = pandas_obj
def query(self, query):
return LLVMGandivaVisitor.gandiva_query(self.pandas_obj, query)
And that is it, now we can use this extension to do things such as:
df = pd.DataFrame({"a": [1.0 * i for i in range(nsize)]})
results = df.gandiva.query("a > 10.0")
As we have registered a Pandas extension called gandiva that is now a first-class citizen of the Pandas DataFrames.
Let’s create now a 5 million floats DataFrame and use the new query() method to filter it:
df = pd.DataFrame({"a": [1.0 * i for i in range(50000000)]})
df.gandiva.query("a < 4.0")
# This will output:
# array([0, 1, 2, 3], dtype=uint32)
Note that the returned values are the indexes satisfying the condition we implemented, so it is different than the Pandas query()that returns the data already filtered.
I did some benchmarks and found that Gandiva is usually always faster than Pandas, however I’ll leave proper benchmarks for a next post on Gandiva as this post was to show how you can use it to JIT expressions.
That’s it ! I hope you liked the post as I enjoyed exploring Gandiva. It seems that we will probably have more and more tools coming up with Gandiva acceleration, specially for SQL parsing/projection/JITing. Gandiva is much more than what I just showed, but you can get started now to understand more of its architecture and how to build the expression trees.
– Christian S. Perone
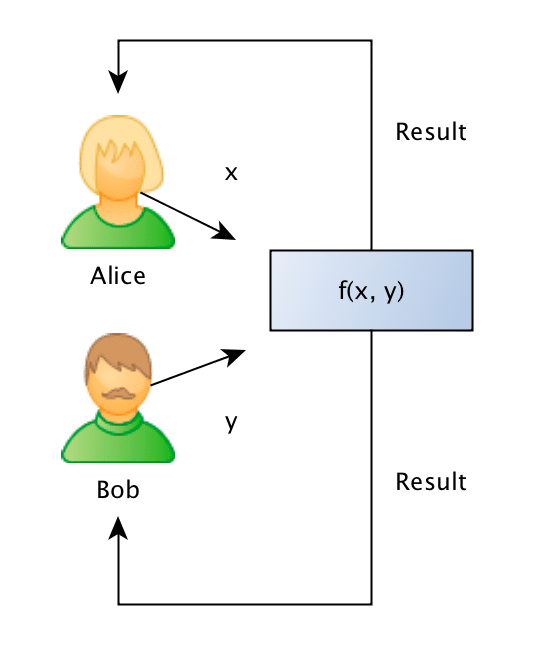
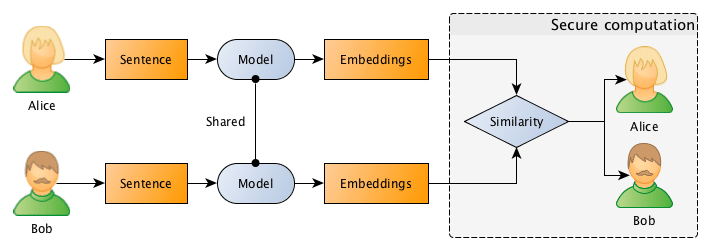
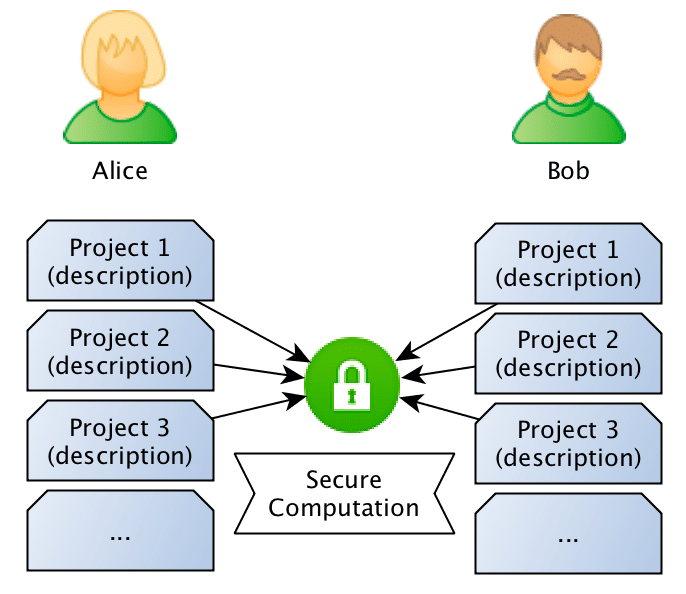What they want to do is to jointly compute the similarity between projects in order to find if they should be doing partnership on a project or not, however, and this is the important point: Bob doesn’t want Alice to know the project descriptions and neither Alice wants Bob to be aware of their projects, they want to know the closest match between the different projects they run, but without disclosing the project ideas (project descriptions).
