Today, I read a news article from the Physorg.com about the new pattern found in the Prime Numbers, the article talks about the new discovery by Bartolo Luque and Lucas Lacasa:
In a recent study, Bartolo Luque and Lucas Lacasa of the Universidad Politécnica de Madrid in Spain have discovered a new pattern in primes that has surprisingly gone unnoticed until now. They found that the distribution of the leading digit in the prime number sequence can be described by a generalization of Benford’s law.
I was very surprised by the fact that nobody have noticed that before and after read the original paper (if you are interested, read it) describing the new patterns discovered, I was very impressed and impatient to see it in pratice !
The new pattern discovered is based on the so-called GBL (Generalized Benford’s Law), which you can see in the paper at the Eq 3.1:
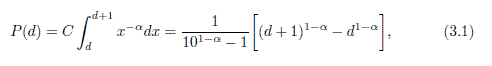
Where the P(d) means the probability of appearance of the leading digit d. The alpha is the exponent of the original power law distribution (for alpha = 1, the GBL reduces to the Benford’s law).
The authors says that for a given integer interval of [1,N], there exists a particular value alpha(N) for which the GBL fits with extremely good accuracy the first digit distribution of the primes appearing in that interval and showing the functional relation between alpha and N in the Eq 3.2:
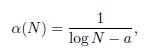
Where a = 1.10 +- 0.05 for large values of N. They also cite a GBL extension, but I’ll use just these formulae to plot our distributions.
So I have implemented these formulae into the simple pybenford module as follows:
def gbl(alpha, digit):
return 1/(10**(1-alpha)-1)*((digit + 1)**(1-alpha)-digit**(1-alpha))
def calc_alpha(n, a=1.10):
return 1/(math.log(n)-a)
def gbenford_law(alpha):
return [gbl(alpha, digit)*100.0 for digit in xrange(1,10)]
For the reason that we are using an infinite integer sequence, we must always pick the sequence interval [1, N] where N = 10^D (see the Natural Density section of the paper for more information).
The next step is to create a list of prime numbers between an arbitrary interval of D=8, or [1,10^8]. In this step I used the Sieve (see more information) utility to create a file with the generated prime numbers in the cited interval, I used the follow command to get this file output:
sieve2310.exe -s 1 -e 100000000 >>sieve_n8.txt
The sieve is very fast, this will create the file “sieve_n8.txt” with nearly 66MB (don’t worry, it’s a very fast generation, it took 8 seconds for me using a Intel Core 2 Duo 2GHz).
And we are ready to use Python and pybenford to read the prime numbers, calculate the leading digits frequency and plot our result ! Here is the code I created:
import pybenford
sieve_file = open("sieve_n8.txt", "r")
prime_list = [int(prime) for prime in sieve_file]
sieve_file.close()
alpha = pybenford.calc_alpha(10**8)
benford_law = pybenford.gbenford_law(alpha)
prime_distribution = pybenford.calc_firstdigit(prime_list)
pybenford.plot_comparative(prime_distribution, benford_law, "Prime Numbers")
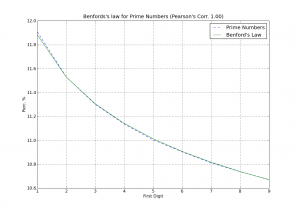
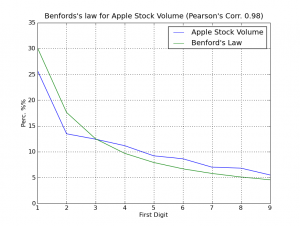
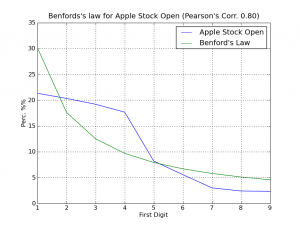
And voilà, here is the output plot showing an extremely good accuracy claimed by paper authors (click on the image to enlarge):
The plotting of the distributions (click to enlarge)
If you are interested on Benford’s law, there are some posts about it here and here.
I hope you liked this =)
UPDATE 10/05: Mike Loukides did a good work generalizing for other bases, thank you for sharing your experiment Mike.
UPDATE 08/08 (lol): There are many more comments about this post on Reddit, see here.