Machine Learning :: Cosine Similarity for Vector Space Models (Part III)
* It has been a long time since I wrote the TF-IDF tutorial (Part I and Part II) and as I promissed, here is the continuation of the tutorial. Unfortunately I had no time to fix the previous tutorials for the newer versions of the scikit-learn (sklearn) package nor to answer all the questions, but I hope to do that in a close future.
So, on the previous tutorials we learned how a document can be modeled in the Vector Space, how the TF-IDF transformation works and how the TF-IDF is calculated, now what we are going to learn is how to use a well-known similarity measure (Cosine Similarity) to calculate the similarity between different documents.
The Dot Product
Let’s begin with the definition of the dot product for two vectors: and
, where
and
are the components of the vector (features of the document, or TF-IDF values for each word of the document in our example) and the
is the dimension of the vectors:
As you can see, the definition of the dot product is a simple multiplication of each component from the both vectors added together. See an example of a dot product for two vectors with 2 dimensions each (2D):
The first thing you probably noticed is that the result of a dot product between two vectors isn’t another vector but a single value, a scalar.
This is all very simple and easy to understand, but what is a dot product ? What is the intuitive idea behind it ? What does it mean to have a dot product of zero ? To understand it, we need to understand what is the geometric definition of the dot product:
Rearranging the equation to understand it better using the commutative property, we have:
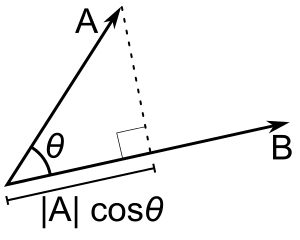
So, what is the term ? This term is the projection of the vector
into the vector
as shown on the image below:
Now, what happens when the vector is orthogonal (with an angle of 90 degrees) to the vector
like on the image below ?
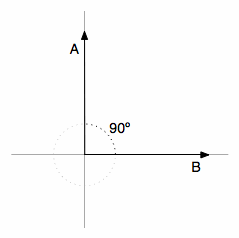
There will be no adjacent side on the triangle, it will be equivalent to zero, the term will be zero and the resulting multiplication with the magnitude of the vector
will also be zero. Now you know that, when the dot product between two different vectors is zero, they are orthogonal to each other (they have an angle of 90 degrees), this is a very neat way to check the orthogonality of different vectors. It is also important to note that we are using 2D examples, but the most amazing fact about it is that we can also calculate angles and similarity between vectors in higher dimensional spaces, and that is why math let us see far than the obvious even when we can’t visualize or imagine what is the angle between two vectors with twelve dimensions for instance.
The Cosine Similarity
The cosine similarity between two vectors (or two documents on the Vector Space) is a measure that calculates the cosine of the angle between them. This metric is a measurement of orientation and not magnitude, it can be seen as a comparison between documents on a normalized space because we’re not taking into the consideration only the magnitude of each word count (tf-idf) of each document, but the angle between the documents. What we have to do to build the cosine similarity equation is to solve the equation of the dot product for the :
And that is it, this is the cosine similarity formula. Cosine Similarity will generate a metric that says how related are two documents by looking at the angle instead of magnitude, like in the examples below:
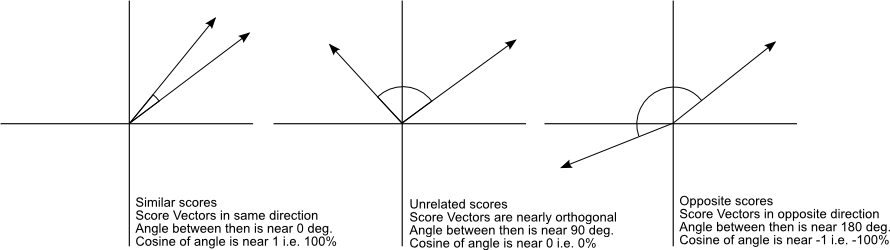
Note that even if we had a vector pointing to a point far from another vector, they still could have an small angle and that is the central point on the use of Cosine Similarity, the measurement tends to ignore the higher term count on documents. Suppose we have a document with the word “sky” appearing 200 times and another document with the word “sky” appearing 50, the Euclidean distance between them will be higher but the angle will still be small because they are pointing to the same direction, which is what matters when we are comparing documents.
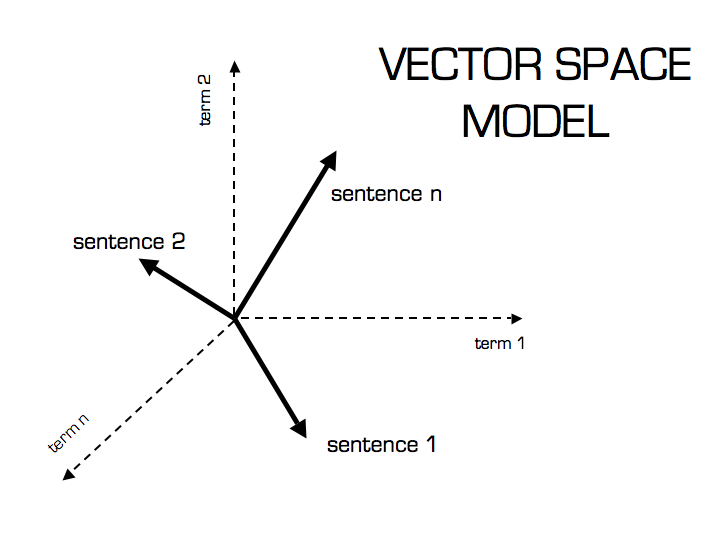
Now that we have a Vector Space Model of documents (like on the image below) modeled as vectors (with TF-IDF counts) and also have a formula to calculate the similarity between different documents in this space, let’s see now how we do it in practice using scikit-learn (sklearn).
Practice Using Scikit-learn (sklearn)
* In this tutorial I’m using the Python 2.7.5 and Scikit-learn 0.14.1.
The first thing we need to do is to define our set of example documents:
documents = ( "The sky is blue", "The sun is bright", "The sun in the sky is bright", "We can see the shining sun, the bright sun" )
And then we instantiate the Sklearn TF-IDF Vectorizer and transform our documents into the TF-IDF matrix:
from sklearn.feature_extraction.text import TfidfVectorizer tfidf_vectorizer = TfidfVectorizer() tfidf_matrix = tfidf_vectorizer.fit_transform(documents) print tfidf_matrix.shape (4, 11)
Now we have the TF-IDF matrix (tfidf_matrix) for each document (the number of rows of the matrix) with 11 tf-idf terms (the number of columns from the matrix), we can calculate the Cosine Similarity between the first document (“The sky is blue”) with each of the other documents of the set:
from sklearn.metrics.pairwise import cosine_similarity cosine_similarity(tfidf_matrix[0:1], tfidf_matrix) array([[ 1. , 0.36651513, 0.52305744, 0.13448867]])
The tfidf_matrix[0:1] is the Scipy operation to get the first row of the sparse matrix and the resulting array is the Cosine Similarity between the first document with all documents in the set. Note that the first value of the array is 1.0 because it is the Cosine Similarity between the first document with itself. Also note that due to the presence of similar words on the third document (“The sun in the sky is bright”), it achieved a better score.
If you want, you can also solve the Cosine Similarity for the angle between vectors:
We only need to isolate the angle () and move the
to the right hand of the equation:
The is the same as the inverse of the cosine (
).
import math # This was already calculated on the previous step, so we just use the value cos_sim = 0.52305744 angle_in_radians = math.acos(cos_sim) print math.degrees(angle_in_radians) 58.462437107432784
And that angle of ~58.5 is the angle between the first and the third document of our document set.
Related Material
A video about Dot Product on The Khan Academy
Scikit-learn (sklearn) – The de facto Machine Learning package for Python

Great tutorial, thanks! One comment and one question 🙂
Comment, in case it helps someone else: a custom tokenizer can be passed to TfidfVectorizer, as explained at http://blog.mafr.de/2012/04/15/scikit-learn-feature-extractio/I had a list of keywords (e.g., “blue car”) I didn’t want to have split into “blue” and “car” and it took me a little while to figure it out.
Question: is there a way to get a list of the features ranked by weight?
just use ngrams (1,3) in tfidf param
The tutorials are incredible. They’ve taught me quite a bit.
Great thanks Sean !
I like your tutorial and approach of measuring the similarity between documents. Have you also tried to apply the same method to find similarity between datasets in the linked data cloud? E.g. finding similar entities between http://dbpedia.org/ and http://www.geonames.org/. Assume you have a location (city) with Zuerich in DBpedia and like to find the same (similar) entity inside geonames.
Great tutorial! Thanks for sharing!
print tfidf_matrix.shape returned a matrix of (21488, 12602) size Which caused a MemoryError. How to handle such matrix of such bigger size as my data keeps on growing. Any Solution Would be a great help
the vectorizer takes in a term called max_features. Limit it to a value, say 5000 or lower, though this would reduce the ability of a vector to uniquely represent a document. Or add some RAM to your machine :-).
Hi, I found your article while I am searching for a simple explanation for cosine similarity but I read the first two articles too when I found that its “tf-idf”. Actually I cant express my feeling after realizing how precisely you have described the concepts both mathematically ans in simple terms. You have explained each and every mathematical notation which is really helpful.
Finally I must thank you for this wonderful tutorial. Please post other machine learning algorithms too in your simple way of expressing them. That would be really helpful.
Great thanks for the feedback Isura. I’ll work on newer tutorials in the near future, just need to get some time to write. See you !
Hi Christian,
It was a great tutorial and I tried to replicate the things you described in the tutorial. However, I keep getting a consistent error which doesn’t allow me to calculate cosine scores…its something like,
from sklearn.metrics.pairwise import cosine_similarity
ImportError: cannot import name cosine_similarity
The same error for TfidfVectorizer. I figured there might be something wrong with sklearn.metrics perhaps? Any help that you can provide on this?
Hello, please note that some parts of the API has changed since I made this tutorial, so check the version you are using.
Thanks for the explanation. I just stumbled into your tutorial while I was googling how to eradicate zero dot product results in getting distance between documents but I don’t understand your tfidf_matrix[0:1]
Also where are the functions.
Thank you
Great thanks for your tutorials.
please, this error appear on terminal
raise ValueError(“empty vocabulary; perhaps the documents only”
ValueError: empty vocabulary; perhaps the documents only contain stop words
why ? what is the solution?
I like ur post, it is pretty clear and detail oriented, thank you for your hard working and sharing!
Excellent tutorials! Very clear and concise, beats the hell out of anything else I’ve read on the topic. Can’t wait until you write more on this topic!
great…………….. tutorial.
Thank You.
Thanks for any other informative web site. Where else may just I get that type of information written in such an ideal approach?I have a
challenge that I am simply now operating on, and I’ve been on thee glance out for sudh info.
Great set of tutorials. Thanks for taking the time to and posting it.
I would really be interested to know how to find the cosine between two different datasets. For instance, how would you find the similarity of the documents in a test set to documents in training set? It’ll be really appreciate it if someone can point me in the right direction.
Thanks, good info here.
I have read all the three tutorials part-I, II, and now III. They are really very good and simple to understand.
Thanks for these great tutorials. i hope to see more similar tutorials on machine learning, which involves python and scikit-learn.
I am getting a memory in using TfidVectorizer.please tell me what could be the reason
memoryerror
|a|cos(th) is not the projection of vector a onto vector b. It is simply the magnitude of the projection on the x-axis. The actual project of vector a onto vector b is |a|cos(th)*B, where B is the unit vector in the direction of B.
Thanks for the blog. The one fundamental element this blog does not explain is the derivation of the following:
\vec{a} \cdot \vec{b} = \|\vec{a}\|\|\vec{b}\|\cos{\theta}
That proof is described here….
https://www.khanacademy.org/math/linear-algebra/vectors_and_spaces/dot_cross_products/v/defining-the-angle-between-vectors
Amazing explanation! Sophisticated simplicity.You saved me loads of time!I can’t thank you enough!
Hello,
I also like you tutorial but I wonder how to fit in my own stopwords. I created a classifier, based on some linguistic theory and for that I had to modify English stopwords. Before evaluating my classifier I would like to conduct a cosine similarity test but do not know how to sneak in my stopwords. 😀
regards,
Guzdeh
Muito bom. Muito obrigado.
Simples e objetivo. Estava a dias quebrando a cabeça para fazer o cálculo do cosseno.
Abraço,
Cristiano.
You saved lots of my time! Thanks.
Hey , thank you very much for this very clear explanation, I had a lot of troubles and you helped me a lot with your post!!!!!!!! You’re great!!!
Incredible tutorial. Learn great knowledge in two minutes reading.
Hi Christian,
I found your explanation of cosine similarity very helpful – especially for a non-maths specialist. I used an excerpt in a presentation I gave at NPPSH (New Perspectives: Postgraduate Symposium for the Humanities) last week (with full attribution).
I would like to use your image explaining cosine similarity in a journal paper based on my presentation and was wondering whether this would be ok? It would, of course, be attributed under the image with full details in the bibliography.
Thank you.
Hi Sara ! You can use without any problems, thanks for citing my article, I’m really glad you liked it.
Thank you so much!
I’m a little confused about the sentence “Also note that due to the presence of similar words on the third document (“The sun in the sky is bright”), it achieved a better score.”
The statement: cosine_similarity(tfidf_matrix[0:1], tfidf_matrix)
produced: array([[ 1. , 0.36651513, 0.52305744, 0.13448867]])
I think your sentence can be interpreted as “The sun in the sky is bright” has “the presence of similar words” to the first document “The sky is blue”. But in the comparison that I see, “The sun in the sky is bright” is more similar to the second document (“The sun is bright”) than to the first document (“The sky is blue”).
Have I missed something?
Colin Goldberg
Hi Colin,
I think you have posted a great question, this also means that you are very careful about code outputs.
Indeed, your remark is well made, but still can be compliant with Cristian Tutorial, because what is written above is the comparison of the first sentence to the others, and you can do the same for the second sentence and get its similarity to the other sentence and get answer you look for, so practically, you can use this code:
from sklearn.metrics.pairwise import cosine_similarity
second_sentence_vector = tfidf_matrix[1:2]
cosine_similarity(second_sentence_vector, tfidf_matrix)
and print the output, you ll have a vector with higher score in third coordinate, which explains your thought.
Hope I made simple for you,
Greetings,
Adil
i want explicit semantic analysis working description
Loved the simplistic approach of the article.
Loved the simplistic approach of the article. Kudos!
awesome article..
A great tutorial series! After more than three years, it is still my #1 place to go, when I want to explain cosine similarity in the context of TF-IDF.
Thanks for the feedback Preslav, it is really nice to hear that.
Please explain how did you get 11 tfidf terms? there are 12 unique terms in the document
Hey, loved this explanation – really clear and insightful, especially the vector space diagrams. Here’s my question, if I have a list of lists of pre tokenized documents (stop words already removed, stemmed using nltk etc.), for example docs = [[“sky”,”blue”],[“sun”,”bright”,”sky”]], how can I feed this into the TfidfVectorizer? It seems that the function can only take raw document strings, but I have already processed my documents and I don’t need TfidfVectorizer to process any more other than to convert the entire set of documents into a tfidf matrix. I keep getting errors such as “TypeError: expected string or bytes-like object”. I suppose I would need to define some of the arguments in TfidfVectorizer such as setting lowercase=False… but nothing has worked so far. Would really appreciate your help, thanks Christian!
Since I can’t delete my original comment (and I still want to praise Christian for his amazing work), I’ll leave this reply here.
Please ignore my original question, I solved it by transforming my list of lists into a tuple XD
Btw, I am using a pandas dataframe called df, where the 7th column of each row is a list of tokens.
code for reference:
tup = ()
for row,index in df.iterrows():
temp = “”
for word in df.iloc[row,7]:
temp = temp + word + ” ”
tup = tup + (temp,)
Thanks for the wonderful explanation .
Nice and neat explanation of cosine similarity. Thanks Christian!
it is a great tutorial
thanks a lot
Hi Christian, thanks for a great tutorial. I have a question:
I have a set of documents that have ID numbers assigned to each of them. The ID is the key and the text is the value in a dictionary format. Once I get an array of similarity scores using the cosine similarity function, how can I know which score belongs to which two documents? Is there something you can put together to pull the document names/IDs along with their cosine similarity score?
Hi Manasa, did you find a solution for names? I’m facing same problem. Thanks!
Thanks a lot Christian
There are many people who know stuff. But there are only a few who can explain what they know, so well.. Kudos Christian… I just chanced upon this from google search and this is awesome…
Thanks for the post! It was exactly what I was looking for. This is weirdly unrelated, but did you take your profile picture in Chania, Crete? The reason I am asking is because I took an almost identical photo there a couple years ago and I swear thats the Chania lighthouse. Perhaps we could use cosine similarity to see how similar the pixels are lmao.
haha hey Trent, I’m glad you liked the post ! The profile picture was exactly on Chania, Crete hehe, what a coincidence ! Amazing place by the way, really liked there, full of history.
Thanks for articulating this. We have all perhaps studied and were excited about these concepts in advanced maths in high school – but hey what a loss in understanding we get to in 20 odd years of professional work. It was quite refreshing to read it – and see how basic ML is relevant as a subject in schools.
Hello Sir, Thanks for this wonderful tutorial (all 3 parts). I got a tonne of information on vectors, similarity and much more concepts. You explained things so nicely that I never find in any of the tutorials in Google. I am thankful that I somehow reach this page. I am new to machine learning. Keep sharing your knowledge and enlight more people like me.
great tutorial. helped me a lot..keep posting 🙂
Dear Christian,
Your three-part tutorials are both an easy to understand lesson and an inspiration. Thank you for your efforts and time to produce them.
Wow ! Great learning. Especially for a beginner like me.. 🙂 Thanks for this post.
How can I test a new string which is not in the dataset for most simillar sentence in the dataset.
By far the best blog series on tf-idf and its implementation in Python. I had gone through so many blog posts and documentation, only to find the same content over and over again. Thanks Christain! Cheers!
Very crisp and clear article on cosine similarity. Very helpful.
Thank you for the wonderful article. It is really helpful for text data analysis.
I am working on ticket mapping with service type.
We have one excel sheet where all diff types of service are listed with Service description.
We receive monthly thousands of tickets with ticket description. Manually it’s not possible to identify each ticket belong to which service.
I tried vector method but getting error bcos both database shape is diff
ValueError: Incompatible dimension for X and Y matrices: X.shape[1] == 52511 while Y.shape[1] == 592
The article definitely deserves ‘thank you’. Thank you for well articulated explaination. Eager to dive into other articles too!!
Ainda útil em 2018. 🙂
Muito obrigado!
Okay, so cosine similarity can be used to know the similarity of the documents. But how can we know which terms contribute the most towards the similarity?
just commenting to thank you for this very clear explanation. thanks!
Obrigada, muito didático! Além da distância do cosseno, você recomendaria qual outra métrica para medir a similaridade entre documentos?
Thank you, amazing explanation! Which other metrics would you recommend for measure the similarity between documents?
Olá, obrigado pelo feedback ! Existem várias distâncias que você pode usar, mas no fim tudo depende do problema. A mais usada depois da distância do cosseno é a distância euclidiana, mas vai praticamente a mesma coisa que a distância de cosseno se você normalizar os vetores.
Thank you for a very detailed and clear explanation of the concepts. You have helped me greatly.
Thanks for the brief and clear explanation of Cosine Similarity … good examples !
Thank you for this, it was extremely clear and understandable. Thanks for all the examples as well.
I have studied several articles about this exact issue, because my docent rushed through it too quickly for me to follow him. None article has explained the TFIDF and cosine similarity so well and thoroughly like you did. You even managed it that I find this whole topic pretty easy now. Thank you very much you helped me *greatly*!
Thanks a lot for the feedback !!!
Thanks very much for the detailed example and explanation!
Hi , Firstly thanks for the great tutorial.
Can we use this for the clothing recommendation system? Like if a user has selected a product with title “Metronaut Men Solid Casual Dark Blue Shirt” and we have this type of title for every other product.So, what I would like to do is recommending the similar products to the above.
Or is there any other method?
Einstein once said that if you aren’t able to simplify the matter, you don’t understand the matter. You, Mr. Perone, do understand the matter.
Much appreciated.
Brilliant , well structured post! Kudos!
Hey man thanks for writing this block helped a lot for my test as well as for my project too. Good work man and thanks again.
Thank for the clear explanation , it really helped
Awesome explanation 🙂 Thanks!
Thank you for the clear explanation
awesome practical example of application of cosine similarity
please you can explain cosine similarty with example.
and i think dot product for any vector V=(v1,v2 ……)
defined as
dp=sqrt(sum(v1^2,v2^2,……));
are this right???
thanks for you explanation.
And when I have more than 10 thousand feature vecotr(512 length), how to speedup to find the biggest cos similarity?
Simple and Well explained Thank you very much
Thank You for the post.. It helped alot
Hi Christian, the concept is very well explained ! So easy to understand with your words.
Your article helped me to build a text matching function and it works. Thanks again !!
Thank you so much for this post… It helps me a lot.
I don’t understand the cos_sim = 0.52305744 part
where was this calculated?
This was the best tutorial i’ve ever read about cosine similarity and tf-idf, finally i understood.