Tag: machine learning

Machine Learning

Feste: composing NLP tasks with automatic parallelization and batching

I just released Feste, a free and open-source framework with a permissive license that allows scalable composition of NLP tasks using a graph execution model that is optimized and executed by specialized schedulers. The main idea behind Feste is that it builds a graph of execution instead of executing tasks immediately, this graph allows Feste to optimize and parallelize it. One main example of optimization is when we have multiple calls to the same backend (e.g. same API), Feste automatically fuses these calls into a single one and therefore it batches the call to reduce latency and improve backend inference leverage of GPU vectorization. Feste also executes tasks that can be done in parallel in different processes, so the user doesn’t have to care about parallelization, especially when there are multiple frameworks using different concurrency strategies.

Project page: https://feste.readthedocs.io/en/latest/design.html
Github: https://github.com/perone/feste

by Christian S. Perone
Machine Learning, Python

Listening to the neural network gradient norms during training

Training neural networks is often done by measuring many different metrics such as accuracy, loss, gradients, etc. This is most of the time done aggregating these metrics and plotting visualizations on TensorBoard.

There are, however, other senses that we can use to monitor the training of neural networks, such as sound. Sound is one of the perspectives that is currently very poorly explored in the training of neural networks. Human hearing can be very good a distinguishing very small perturbations in characteristics such as rhythm and pitch, even when these perturbations are very short in time or subtle.

For this experiment, I made a very simple example showing a synthesized sound that was made using the gradient norm of each layer and for step of the training for a convolutional neural network training on MNIST using different settings such as different learning rates, optimizers, momentum, etc.

You’ll need to install PyAudio and PyTorch to run the code (in the end of this post).

Training sound with SGD using LR 0.01

This segment represents a training session with gradients from 4 layers during the first 200 steps of the first epoch and using a batch size of 10. The higher the pitch, the higher the norm for a layer, there is a short silence to indicate different batches. Note the gradient increasing during time.

Training sound with SGD using LR 0.1

Same as above, but with higher learning rate.

Training sound with SGD using LR 1.0

Same as above, but with high learning rate that makes the network to diverge, pay attention to the high pitch when the norms explode and then divergence.

Training sound with SGD using LR 1.0 and BS 256

Same setting but with a high learning rate of 1.0 and a batch size of 256. Note how the gradients explode and then there are NaNs causing the final sound.

Training sound with Adam using LR 0.01

This is using Adam in the same setting as the SGD.

 

Source code

For those who are interested, here is the entire source code I used to make the sound clips:

import pyaudio
import numpy as np
import wave

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 50, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

        self.ordered_layers = [self.conv1,
                               self.conv2,
                               self.fc1,
                               self.fc2]

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2, 2)
        x = x.view(-1, 4*4*50)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)


def open_stream(fs):
    p = pyaudio.PyAudio()
    stream = p.open(format=pyaudio.paFloat32,
                    channels=1,
                    rate=fs,
                    output=True)
    return p, stream


def generate_tone(fs, freq, duration):
    npsin = np.sin(2 * np.pi * np.arange(fs*duration) * freq / fs)
    samples = npsin.astype(np.float32)
    return 0.1 * samples


def train(model, device, train_loader, optimizer, epoch):
    model.train()

    fs = 44100
    duration = 0.01
    f = 200.0
    p, stream = open_stream(fs)

    frames = []

    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()

        norms = []
        for layer in model.ordered_layers:
            norm_grad = layer.weight.grad.norm()
            norms.append(norm_grad)

            tone = f + ((norm_grad.numpy()) * 100.0)
            tone = tone.astype(np.float32)
            samples = generate_tone(fs, tone, duration)

            frames.append(samples)

        silence = np.zeros(samples.shape[0] * 2,
                           dtype=np.float32)
        frames.append(silence)

        optimizer.step()

        # Just 200 steps per epoach
        if batch_idx == 200:
            break

    wf = wave.open("sgd_lr_1_0_bs256.wav", 'wb')
    wf.setnchannels(1)
    wf.setsampwidth(p.get_sample_size(pyaudio.paFloat32))
    wf.setframerate(fs)
    wf.writeframes(b''.join(frames))
    wf.close()

    stream.stop_stream()
    stream.close()
    p.terminate()


def run_main():
    device = torch.device("cpu")

    train_loader = torch.utils.data.DataLoader(
        datasets.MNIST('../data', train=True, download=True,
                       transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=256, shuffle=True)

    model = Net().to(device)
    optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

    for epoch in range(1, 2):
        train(model, device, train_loader, optimizer, epoch)


if __name__ == "__main__":
    run_main()
Cite this article as: Christian S. Perone, "Listening to the neural network gradient norms during training," in Terra Incognita, 04/08/2019, https://blog.christianperone.com/2019/08/listening-to-the-neural-network-gradient-norms-during-training/.
by Christian S. Perone
Machine Learning

Benford law on GPT-2 language model

I wrote some months ago about how the Benford law emerges from language models, today I decided to evaluate the same method to check how the GPT-2 would behave with some sentences and it turns out that it seems that it is also capturing these power laws. You can find some plots with the examples below, the plots are showing the probability of the digit given a particular sentence such as “with a population size of”, showing the distribution of: $$P(\{1,2, \ldots, 9\} \vert \text{“with a population size of”})$$ for the GPT-2 medium model (345M):

Cite this article as: Christian S. Perone, "Benford law on GPT-2 language model," in Terra Incognita, 14/06/2019, https://blog.christianperone.com/2019/06/benford-law-on-gpt-2-language-model/.

by Christian S. Perone
Machine Learning

Introducing EuclidesDB – A machine learning feature database

Past week I released the first public version of EuclidesDB. EuclidesDB is a multi-model machine learning feature database that is tightly coupled with PyTorch and provides a backend for including and querying data on the model feature space.

For more information, see the GitHub repository or the documentation.

Some features of EuclidesDB are listed below:

  • Written in C++ for performance;
  • Uses protobuf for data serialization;
  • Uses gRPC for communication;
  • LevelDB integration for database serialization;
  • Many indexing methods implemented (Annoy, Faiss, etc);
  • Tight PyTorch integration through libtorch;
  • Easy integration for new custom fine-tuned models;
  • Easy client language binding generation;
  • Free and open-source with permissive license;

And here is a diagram of the overall architecture:

by Christian S. Perone
Machine Learning

Benford’s law emerges from deep language model

I was experimenting with the digits distribution from a pre-trained (weights from the OpenAI repository) Transformer language model (LM) and I found a very interesting correlation between the Benford’s law and the digit distribution of the language model after conditioning it with some particular phrases.

Below is the correlation between the Benford’s law and the language model with conditioning on the phrase (shown in the figure):

 

by Christian S. Perone
Machine Learning, Python

PyTorch 1.0 tracing JIT and LibTorch C++ API to integrate PyTorch into NodeJS

Update 28 Feb 2019: I added a new blog post with a slide deck containing the presentation I did for PyData Montreal.

Today, at the PyTorch Developer Conference, the PyTorch team announced the plans and the release of the PyTorch 1.0 preview with many nice features such as a JIT for model graphs (with and without tracing) as well as the LibTorch, the PyTorch C++ API, one of the most important release announcement made today in my opinion.

Given the huge interest in understanding how this new API works, I decided to write this article showing an example of many opportunities that are now open after the release of the PyTorch C++ API. In this post, I’ll integrate PyTorch inference into native NodeJS using NodeJS C++ add-ons, just as an example of integration between different frameworks/languages that are now possible using the C++ API.

Below you can see the final result:

As you can see, the integration is seamless and I could use a traced ResNet as the computational graph model and feed any tensor to it to get the output predictions.

Introduction

Simply put, the libtorch is a library version of the PyTorch. It contains the underlying foundation that is used by PyTorch, such as the ATen (the tensor library), which contains all the tensor operations and methods. Libtorch also contains the autograd, which is the component that adds the automatic differentiation to the ATen tensors.

A word of caution for those who are starting now is to be careful with the use of the tensors that can be created both from ATen and autograd, do not mix them, the ATen will return the plain tensors (when you create them using the at namespace) while the autograd functions (from the torch namespace) will return Variable, by adding its automatic differentiation mechanism.

For a more extensive tutorial on how PyTorch internals work, please take a look on my previous tutorial on the PyTorch internal architecture.

Libtorch can be downloaded from the Pytorch website and it is only available as a preview for a while. You can also find the documentation in this site, which is mostly a Doxygen rendered documentation. I found the library pretty stable, and it makes sense because it is actually exposing the stable foundations of PyTorch, however, there are some issues with headers and some minor problems concerning the library organization that you might find while starting working with it (that will hopefully be fixed soon).

For NodeJS, I’ll use the Native Abstractions library (nan) which is the most recommended library (actually is basically a header-only library) to create NodeJS C++ add-ons and the cmake-js, because libtorch already provide the cmake files that make our building process much easier. However, the focus here will be on the C++ code and not on the building process.

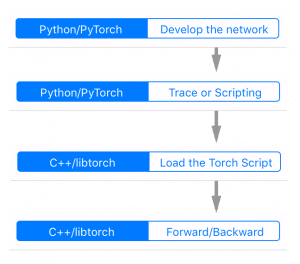
The flow for the development, tracing, serializing and loading the model can be seen in the figure on the left side.

It starts with the development process and tracing being done in PyTorch (Python domain) and then the loading and inference on the C++ domain (in our case in NodeJS add-on).

 

Wrapping the Tensor

In NodeJS, to create an object as a first-class citizen of the JavaScript world, you need to inherit from the ObjectWrap class, which will be responsible for wrapping a C++ component.

#ifndef TENSOR_H
#define TENSOR_H

#include <nan.h>
#include <torch/torch.h>

namespace torchjs {

class Tensor : public Nan::ObjectWrap {
 public:
  static NAN_MODULE_INIT(Init);

  void setTensor(at::Tensor tensor) {
    this->mTensor = tensor;
  }

  torch::Tensor getTensor() {
    return this->mTensor;
  }

  static v8::Local<v8::Object> NewInstance();

 private:
  explicit Tensor();
  ~Tensor();

  static NAN_METHOD(New);
  static NAN_METHOD(toString);
  static Nan::Persistent<v8::Function> constructor;

 private:
  torch::Tensor mTensor;

};

}  // namespace torchjs

#endif

As you can see, most of the code for the definition of our Tensor class is just boilerplate. The key point here is that the torchjs::Tensor will wrap a torch::Tensor and we added two special public methods (setTensor and getTensor) to set and get this internal torch tensor.

I won’t show all the implementation details because most parts of it are NodeJS boilerplate code to construct the object, etc. I’ll focus on the parts that touch the libtorch API, like in the code below where we are creating a small textual representation of the tensor to show on JavaScript (toString method):

NAN_METHOD(Tensor::toString) {
  Tensor* obj = ObjectWrap::Unwrap<Tensor>(info.Holder());
  std::stringstream ss;

  at::IntList sizes = obj->mTensor.sizes();
  ss << "Tensor[Type=" << obj->mTensor.type() << ", ";
  ss << "Size=" << sizes << std::endl;

  info.GetReturnValue().Set(Nan::New(ss.str()).ToLocalChecked());
}

What we are doing in the code above, is just getting the internal tensor object from the wrapped object by unwrapping it. After that, we build a string representation with the tensor size (each dimension sizes) and its type (float, etc).

Wrapping Tensor-creation operations

Let’s create now a wrapper code for the torch::ones function which is responsible for creating a tensor of any defined shape filled with constant 1’s.

NAN_METHOD(ones) {
  // Sanity checking of the arguments
  if (info.Length() < 2)
    return Nan::ThrowError(Nan::New("Wrong number of arguments").ToLocalChecked());

  if (!info[0]->IsArray() || !info[1]->IsBoolean())
    return Nan::ThrowError(Nan::New("Wrong argument types").ToLocalChecked());

  // Retrieving parameters (require_grad and tensor shape)
  const bool require_grad = info[1]->BooleanValue();
  const v8::Local<v8::Array> array = info[0].As<v8::Array>();
  const uint32_t length = array->Length();

  // Convert from v8::Array to std::vector
  std::vector<long long> dims;
  for(int i=0; i<length; i++)
  {
    v8::Local<v8::Value> v;
    int d = array->Get(i)->NumberValue();
    dims.push_back(d);
  }

  // Call the libtorch and create a new torchjs::Tensor object
  // wrapping the new torch::Tensor that was created by torch::ones
  at::Tensor v = torch::ones(dims, torch::requires_grad(require_grad));
  auto newinst = Tensor::NewInstance();
  Tensor* obj = Nan::ObjectWrap::Unwrap<Tensor>(newinst);
  obj->setTensor(v);

  info.GetReturnValue().Set(newinst);
}

So, let’s go through this code. We are first checking the arguments of the function. For this function, we’re expecting a tuple (a JavaScript array) for the tensor shape and a boolean indicating if we want to compute gradients or not for this tensor node. After that, we’re converting the parameters from the V8 JavaScript types into native C++ types. Soon as we have the required parameters, we then call the torch::ones function from the libtorch, this function will create a new tensor where we use a torchjs::Tensor class that we created earlier to wrap it.

And that’s it, we just exposed one torch operation that can be used as native JavaScript operation.

Intermezzo for the PyTorch JIT

The introduced PyTorch JIT revolves around the concept of the Torch Script. A Torch Script is a restricted subset of the Python language and comes with its own compiler and transform passes (optimizations, etc).

This script can be created in two different ways: by using a tracing JIT or by providing the script itself. In the tracing mode, your computational graph nodes will be visited and operations recorded to produce the final script, while the scripting is the mode where you provide this description of your model taking into account the restrictions of the Torch Script.

Note that if you have branching decisions on your code that depends on external factors or data, tracing won’t work as you expect because it will record that particular execution of the graph, hence the alternative option to provide the script. However, in most of the cases, the tracing is what we need.

To understand the differences, let’s take a look at the Intermediate Representation (IR) from the script module generated both by tracing and by scripting.

@torch.jit.script
def happy_function_script(x):
    ret = torch.rand(0)
    if True == True:
        ret = torch.rand(1)
    else:
        ret = torch.rand(2)
    return ret

def happy_function_trace(x):
    ret = torch.rand(0)
    if True == True:
        ret = torch.rand(1)
    else:
        ret = torch.rand(2)
    return ret

traced_fn = torch.jit.trace(happy_function_trace,
                            (torch.tensor(0),),
                            check_trace=False)

In the code above, we’re providing two functions, one is using the @torch.jit.script decorator, and it is the scripting way to create a Torch Script, while the second function is being used by the tracing function torch.jit.trace. Not that I intentionally added a “True == True” decision on the functions (which will always be true).

Now, if we inspect the IR generated by these two different approaches, we’ll clearly see the difference between the tracing and scripting approaches:

# 1) Graph from the scripting approach
graph(%x : Dynamic) {
  %16 : int = prim::Constant[value=2]()
  %10 : int = prim::Constant[value=1]()
  %7 : int = prim::Constant[value=1]()
  %8 : int = prim::Constant[value=1]()
  %9 : int = aten::eq(%7, %8)
  %ret : Dynamic = prim::If(%9)
    block0() {
      %11 : int[] = prim::ListConstruct(%10)
      %12 : int = prim::Constant[value=6]()
      %13 : int = prim::Constant[value=0]()
      %14 : int[] = prim::Constant[value=[0, -1]]()
      %ret.2 : Dynamic = aten::rand(%11, %12, %13, %14)
      -> (%ret.2)
    }
    block1() {
      %17 : int[] = prim::ListConstruct(%16)
      %18 : int = prim::Constant[value=6]()
      %19 : int = prim::Constant[value=0]()
      %20 : int[] = prim::Constant[value=[0, -1]]()
      %ret.3 : Dynamic = aten::rand(%17, %18, %19, %20)
      -> (%ret.3)
    }
  return (%ret);
}

# 2) Graph from the tracing approach
graph(%0 : Long()) {
  %7 : int = prim::Constant[value=1]()
  %8 : int[] = prim::ListConstruct(%7)
  %9 : int = prim::Constant[value=6]()
  %10 : int = prim::Constant[value=0]()
  %11 : int[] = prim::Constant[value=[0, -1]]()
  %12 : Float(1) = aten::rand(%8, %9, %10, %11)
  return (%12);
}

​

As we can see, the IR is very similar to the LLVM IR, note that in the tracing approach, the trace recorded contains only one path from the code, the truth path, while in the scripting we have both branching alternatives. However, even in scripting, the always false branch can be optimized and removed with a dead code elimination transform pass.

PyTorch JIT has a lot of transformation passes that are used to do loop unrolling, dead code elimination, etc. You can find these passes here. Not that conversion to other formats such as ONNX can be implemented as a pass on top of this intermediate representation (IR), which is quite convenient.

Tracing the ResNet

Now, before implementing the Script Module in NodeJS, let’s first trace a ResNet network using PyTorch (using just Python):

traced_net = torch.jit.trace(torchvision.models.resnet18(),
                             torch.rand(1, 3, 224, 224))
traced_net.save("resnet18_trace.pt")

As you can see from the code above, we just have to provide a tensor example (in this case a batch of a single image with 3 channels and size 224×224. After that we just save the traced network into a file called resnet18_trace.pt.

Now we’re ready to implement the Script Module in NodeJS in order to load this file that was traced.

Wrapping the Script Module

This is now the implementation of the Script Module in NodeJS:

// Class constructor
ScriptModule::ScriptModule(const std::string filename) {
  // Load the traced network from the file
  this->mModule = torch::jit::load(filename);
}

// JavaScript object creation
NAN_METHOD(ScriptModule::New) {
  if (info.IsConstructCall()) {
    // Get the filename parameter
    v8::String::Utf8Value param_filename(info[0]->ToString());
    const std::string filename = std::string(*param_filename);

    // Create a new script module using that file name
    ScriptModule *obj = new ScriptModule(filename);
    obj->Wrap(info.This());
    info.GetReturnValue().Set(info.This());
  } else {
    v8::Local<v8::Function> cons = Nan::New(constructor);
    info.GetReturnValue().Set(Nan::NewInstance(cons).ToLocalChecked());
  }
}

As you can see from the code above, we’re just creating a class that will call the torch::jit::load function passing a file name of the traced network. We also have the implementation of the JavaScript object, where we convert parameters to C++ types and then create a new instance of the torchjs::ScriptModule.

The wrapping of the forward pass is also quite straightforward:

NAN_METHOD(ScriptModule::forward) {
  ScriptModule* script_module = ObjectWrap::Unwrap<ScriptModule>(info.Holder());
  Nan::MaybeLocal<v8::Object> maybe = Nan::To<v8::Object>(info[0]);

  Tensor *tensor =
    Nan::ObjectWrap::Unwrap<Tensor>(maybe.ToLocalChecked());
  
  torch::Tensor torch_tensor = tensor->getTensor();
  torch::Tensor output = script_module->mModule->forward({torch_tensor}).toTensor();

  auto newinst = Tensor::NewInstance();
  Tensor* obj = Nan::ObjectWrap::Unwrap<Tensor>(newinst);
  obj->setTensor(output);
  info.GetReturnValue().Set(newinst);
}

As you can see, in this code, we just receive a tensor as an argument, we get the internal torch::Tensor from it and then call the forward method from the script module, we wrap the output on a new torchjs::Tensor and then return it.

And that’s it, we’re ready to use our built module in native NodeJS as in the example below:

var torchjs = require("./build/Release/torchjs");
var script_module = new torchjs.ScriptModule("resnet18_trace.pt");
var data = torchjs.ones([1, 3, 224, 224], false);
var output = script_module.forward(data);

I hope you enjoyed ! Libtorch opens the door for the tight integration of PyTorch in many different languages and frameworks, which is quite exciting and a huge step towards the direction of production deployment code.

– Christian S. Perone

Cite this article as: Christian S. Perone, "PyTorch 1.0 tracing JIT and LibTorch C++ API to integrate PyTorch into NodeJS," in Terra Incognita, 02/10/2018, https://blog.christianperone.com/2018/10/pytorch-1-0-tracing-jit-and-libtorch-c-api-to-integrate-pytorch-into-nodejs/.
by Christian S. Perone
Machine Learning, Math, Probability

Concentration inequalities – Part I

Introduction

Concentration inequalities, or probability bounds, are very important tools for the analysis of Machine Learning algorithms or randomized algorithms. In statistical learning theory, we often want to show that random variables, given some assumptions, are close to its expectation with high probability. This article provides an overview of the most basic inequalities in the analysis of these concentration measures.

Markov’s Inequality

The Markov’s inequality is one of the most basic bounds and it assumes almost nothing about the random variable. The assumptions that Markov’s inequality makes is that the random variable \(X\) is non-negative \(X > 0\) and has a finite expectation \(\mathbb{E}\left[X\right] < \infty\). The Markov’s inequality is given by:

$$\underbrace{P(X \geq \alpha)}_{\text{Probability of being greater than constant } \alpha} \leq \underbrace{\frac{\mathbb{E}\left[X\right]}{\alpha}}_{\text{Bounded above by expectation over constant } \alpha}$$

What this means is that the probability that the random variable \(X\) will be bounded by the expectation of \(X\) divided by the constant \(\alpha\). What is remarkable about this bound, is that it holds for any distribution with positive values and it doesn’t depend on any feature of the probability distribution, it only requires some weak assumptions and its first moment, the expectation.

Example: A grocery store sells an average of 40 beers per day (it’s summer !). What is the probability that it will sell 80 or more beers tomorrow ?

$$
\begin{align}
P(X \geq \alpha) & \leq\frac{\mathbb{E}\left[X\right]}{\alpha} \\\\
P(X \geq 80) & \leq\frac{40}{80} = 0.5 = 50\%
\end{align}
$$

The Markov’s inequality doesn’t depend on any property of the random variable probability distribution, so it’s obvious that there are better bounds to use if information about the probability distribution is available.

Chebyshev’s Inequality

When we have information about the underlying distribution of a random variable, we can take advantage of properties of this distribution to know more about the concentration of this variable. Let’s take for example a normal distribution with mean \(\mu = 0\) and unit standard deviation \(\sigma = 1\) given by the probability density function (PDF) below:

$$ f(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2} $$

Integrating from -1 to 1: \(\int_{-1}^{1} \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\), we know that 68% of the data is within \(1\sigma\) (one standard deviation) from the mean \(\mu\) and 95% is within \(2\sigma\) from the mean. However, when it’s not possible to assume normality, any other amount of data can be concentrated within \(1\sigma\) or \(2\sigma\).

Chebyshev’s inequality provides a way to get a bound on the concentration for any distribution, without assuming any underlying property except a finite mean and variance. Chebyshev’s also holds for any random variable, not only for non-negative variables as in Markov’s inequality.

The Chebyshev’s inequality is given by the following relation:

$$
P( \mid X – \mu \mid \geq k\sigma) \leq \frac{1}{k^2}
$$

that can also be rewritten as:

$$
P(\mid X – \mu \mid < k\sigma) \geq 1 – \frac{1}{k^2}
$$

For the concrete case of \(k = 2\), the Chebyshev’s tells us that at least 75% of the data is concentrated within 2 standard deviations of the mean. And this holds for any distribution.

Now, when we compare this result for \( k = 2 \) with the 95% concentration of the normal distribution for \(2\sigma\), we can see how conservative is the Chebyshev’s bound. However, one must not forget that this holds for any distribution and not only for a normally distributed random variable, and all that Chebyshev’s needs, is the first and second moments of the data. Something important to note is that in absence of more information about the random variable, this cannot be improved.

Chebyshev’s Inequality and the Weak Law of Large Numbers

Chebyshev’s inequality can also be used to prove the weak law of large numbers, which says that the sample mean converges in probability towards the true mean.

That can be done as follows:

  • Consider a sequence of i.i.d. (independent and identically distributed) random variables \(X_1, X_2, X_3, \ldots\) with mean \(\mu\) and variance \(\sigma^2\);
  • The sample mean is \(M_n = \frac{X_1 + \ldots + X_n}{n}\) and the true mean is \(\mu\);
  • For the expectation of the sample mean we have: $$\mathbb{E}\left[M_n\right] = \frac{\mathbb{E}\left[X_1\right] + \ldots +\mathbb{E}\left[X_n\right]}{n} = \frac{n\mu}{n} = \mu$$
  • For the variance of the sample we have: $$Var\left[M_n\right] = \frac{Var\left[X_1\right] + \ldots +Var\left[X_n\right]}{n^2} = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}$$
  • By the application of the Chebyshev’s inequality we have: $$ P(\mid M_n – \mu \mid \geq \epsilon) \leq \frac{\sigma^2}{n\epsilon^2}$$ for any (fixed) \(\epsilon > 0\), as \(n\) increases, the right side of the inequality goes to zero. Intuitively, this means that for a large \(n\) the concentration of the distribution of \(M_n\) will be around \(\mu\).

Improving on Markov’s and Chebyshev’s with Chernoff Bounds

Before getting into the Chernoff bound, let’s understand the motivation behind it and how one can improve on Chebyshev’s bound. To understand it, we first need to understand the difference between a pairwise independence and mutual independence. For the pairwise independence, we have the following for A, B, and C:

$$
P(A \cap B) = P(A)P(B) \\
P(A \cap C) = P(A)P(C) \\
P(B \cap C) = P(B)P(C)
$$

Which means that any pair (any two events) are independent, but not necessarily that:

$$
P(A \cap B\cap C) = P(A)P(B)P(C)
$$

which is called “mutual independence” and it is a stronger independence. By definition, the mutual independence assumes the pairwise independence but the opposite isn’t always true. And this is the case where we can improve on Chebyshev’s bound, as it is not possible without doing these further assumptions (stronger assumptions leads to stronger bounds).

We’ll talk about the Chernoff bounds in the second part of this tutorial !

Cite this article as: Christian S. Perone, "Concentration inequalities – Part I," in Terra Incognita, 23/08/2018, https://blog.christianperone.com/2018/08/concentration-inequalities-part-i/.
by Christian S. Perone