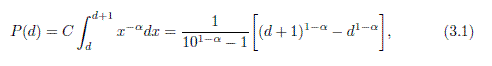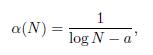From a publication of 28/10/2010, of the authors Saoshi Sasaki, Alexis J Comber, Hiroshi Suzuki and Chris Brunsdon:
Background
Ambulance response time is a crucial factor in patient survival. The number of emergency cases (EMS cases) requiring an ambulance is increasing due to changes in population demographics. This is decreasing ambulance response times to the emergency scene. This paper predicts EMS cases for 5-year intervals from 2020, to 2050 by correlating current EMS cases with demographic factors at the level of the census area and predicted population changes. It then applies a modified grouping genetic algorithm to compare current and future optimal locations and numbers of ambulances. Sets of potential locations were evaluated in terms of the (current and predicted) EMS case distances to those locations.
Results
Future EMS demands were predicted to increase by 2030 using the model (R2=0.71). The optimal locations of ambulances based on future EMS cases were compared with current locations and with optimal locations modelled on current EMS case data. Optimising the location of ambulance stations locations reduced the average response times by 57 seconds. Current and predicted future EMS demand at modelled locations were calculated and compared.
Conclusions
The reallocation of ambulances to optimal locations improved response times and could contribute to higher survival rates from life-threatening medical events. Modelling EMS case ‘demand’ over census areas allows the data to be correlated to population characteristics and optimal ‘supply’ locations to be identified. Comparing current and future optimal scenarios allows more nuanced planning decisions to be made. This is a generic methodology that could be used to provide evidence in support of public health planning and decision making.
Read the original paper here.