Just published this deck of slides of a presentation about Deep Learning and Convolutional Neural Networks.
by Christian S. Perone
Just published this deck of slides of a presentation about Deep Learning and Convolutional Neural Networks.
Convolutional neural networks (or ConvNets) are biologically-inspired variants of MLPs, they have different kinds of layers and each different layer works different than the usual MLP layers. If you are interested in learning more about ConvNets, a good course is the CS231n – Convolutional Neural Newtorks for Visual Recognition. The architecture of the CNNs are shown in the images below:
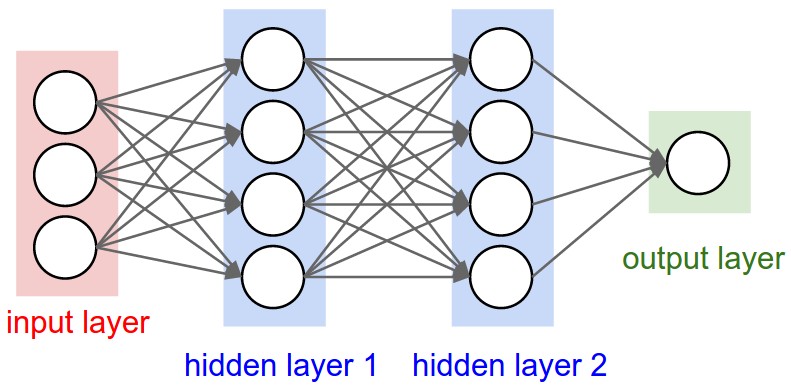
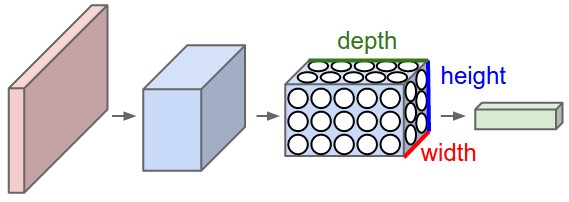
As you can see, the ConvNets works with 3D volumes and transformations of these 3D volumes. I won’t repeat in this post the entire CS231n tutorial, so if you’re really interested, please take time to read before continuing.
One of the Python packages for deep learning that I really like to work with is Lasagne and nolearn. Lasagne is based on Theano so the GPU speedups will really make a great difference, and their declarative approach for the neural networks creation are really helpful. The nolearn libary is a collection of utilities around neural networks packages (including Lasagne) that can help us a lot during the creation of the neural network architecture, inspection of the layers, etc.
What I’m going to show in this post, is how to build a simple ConvNet architecture with some convolutional and pooling layers. I’m also going to show how you can use a ConvNet to train a feature extractor and then use it to extract features before feeding them into different models like SVM, Logistic Regression, etc. Many people use pre-trained ConvNet models and then remove the last output layer to extract the features from ConvNets that were trained on ImageNet datasets. This is usually called transfer learning because you can use layers from other ConvNets as feature extractors for different problems, since the first layer filters of the ConvNets works as edge detectors, they can be used as general feature detectors for other problems.
The MNIST dataset is one of the most traditional datasets for digits classification. We will use a pickled version of it for Python, but first, lets import the packages that we will need to use:
import matplotlib import matplotlib.pyplot as plt import matplotlib.cm as cm from urllib import urlretrieve import cPickle as pickle import os import gzip import numpy as np import theano import lasagne from lasagne import layers from lasagne.updates import nesterov_momentum from nolearn.lasagne import NeuralNet from nolearn.lasagne import visualize from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix
As you can see, we are importing matplotlib for plotting some images, some native Python modules to download the MNIST dataset, numpy, theano, lasagne, nolearn and some scikit-learn functions for model evaluation.
After that, we define our MNIST loading function (this is pretty the same function used in the Lasagne tutorial):
def load_dataset():
url = 'http://deeplearning.net/data/mnist/mnist.pkl.gz'
filename = 'mnist.pkl.gz'
if not os.path.exists(filename):
print("Downloading MNIST dataset...")
urlretrieve(url, filename)
with gzip.open(filename, 'rb') as f:
data = pickle.load(f)
X_train, y_train = data[0]
X_val, y_val = data[1]
X_test, y_test = data[2]
X_train = X_train.reshape((-1, 1, 28, 28))
X_val = X_val.reshape((-1, 1, 28, 28))
X_test = X_test.reshape((-1, 1, 28, 28))
y_train = y_train.astype(np.uint8)
y_val = y_val.astype(np.uint8)
y_test = y_test.astype(np.uint8)
return X_train, y_train, X_val, y_val, X_test, y_test
As you can see, we are downloading the MNIST pickled dataset and then unpacking it into the three different datasets: train, validation and test. After that we reshape the image contents to prepare them to input into the Lasagne input layer later and we also convert the numpy array types to uint8 due to the GPU/theano datatype restrictions.
After that, we’re ready to load the MNIST dataset and inspect it:
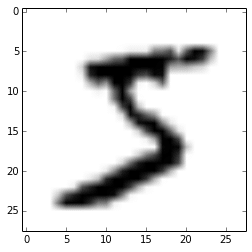
X_train, y_train, X_val, y_val, X_test, y_test = load_dataset() plt.imshow(X_train[0][0], cmap=cm.binary)
This code above will output the following image (I’m using IPython Notebook):
Now we can define our ConvNet architecture and then train it using a GPU/CPU (I have a very cheap GPU, but it helps a lot):
net1 = NeuralNet(
layers=[('input', layers.InputLayer),
('conv2d1', layers.Conv2DLayer),
('maxpool1', layers.MaxPool2DLayer),
('conv2d2', layers.Conv2DLayer),
('maxpool2', layers.MaxPool2DLayer),
('dropout1', layers.DropoutLayer),
('dense', layers.DenseLayer),
('dropout2', layers.DropoutLayer),
('output', layers.DenseLayer),
],
# input layer
input_shape=(None, 1, 28, 28),
# layer conv2d1
conv2d1_num_filters=32,
conv2d1_filter_size=(5, 5),
conv2d1_nonlinearity=lasagne.nonlinearities.rectify,
conv2d1_W=lasagne.init.GlorotUniform(),
# layer maxpool1
maxpool1_pool_size=(2, 2),
# layer conv2d2
conv2d2_num_filters=32,
conv2d2_filter_size=(5, 5),
conv2d2_nonlinearity=lasagne.nonlinearities.rectify,
# layer maxpool2
maxpool2_pool_size=(2, 2),
# dropout1
dropout1_p=0.5,
# dense
dense_num_units=256,
dense_nonlinearity=lasagne.nonlinearities.rectify,
# dropout2
dropout2_p=0.5,
# output
output_nonlinearity=lasagne.nonlinearities.softmax,
output_num_units=10,
# optimization method params
update=nesterov_momentum,
update_learning_rate=0.01,
update_momentum=0.9,
max_epochs=10,
verbose=1,
)
# Train the network
nn = net1.fit(X_train, y_train)
As you can see, in the parameter layers we’re defining a dictionary of tuples with the layer names/types and then we define the parameters for these layers. Our architecture here is using two convolutional layers with poolings and then a fully connected layer (dense layer) and the output layer. There are also dropouts between some layers, the dropout layer is a regularizer that randomly sets input values to zero to avoid overfitting (see the image below).
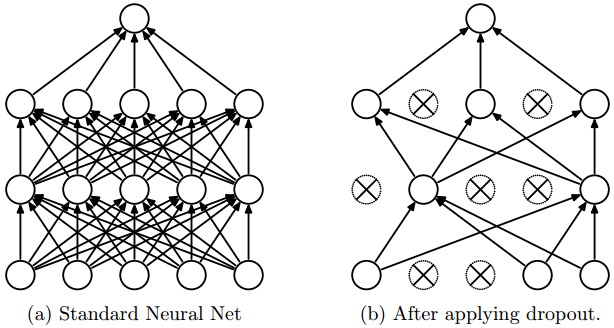
After calling the train method, the nolearn package will show status of the learning process, in my machine with my humble GPU I got the results below:
# Neural Network with 160362 learnable parameters
## Layer information
# name size
--- -------- --------
0 input 1x28x28
1 conv2d1 32x24x24
2 maxpool1 32x12x12
3 conv2d2 32x8x8
4 maxpool2 32x4x4
5 dropout1 32x4x4
6 dense 256
7 dropout2 256
8 output 10
epoch train loss valid loss train/val valid acc dur
------- ------------ ------------ ----------- --------- ---
1 0.85204 0.16707 5.09977 0.95174 33.71s
2 0.27571 0.10732 2.56896 0.96825 33.34s
3 0.20262 0.08567 2.36524 0.97488 33.51s
4 0.16551 0.07695 2.15081 0.97705 33.50s
5 0.14173 0.06803 2.08322 0.98061 34.38s
6 0.12519 0.06067 2.06352 0.98239 34.02s
7 0.11077 0.05532 2.00254 0.98427 33.78s
8 0.10497 0.05771 1.81898 0.98248 34.17s
9 0.09881 0.05159 1.91509 0.98407 33.80s
10 0.09264 0.04958 1.86864 0.98526 33.40s
As you can see, the accuracy in the end was 0.98526, a pretty good performance for a 10 epochs training.
Now we can use the model to predict the entire testing dataset:
preds = net1.predict(X_test)
And we can also plot a confusion matrix to check the performance of the neural network classification:
cm = confusion_matrix(y_test, preds)
plt.matshow(cm)
plt.title('Confusion matrix')
plt.colorbar()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
The code above will plot the following confusion matrix:
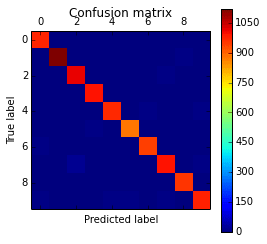
As you can see, the diagonal is where the classification is more dense, showing the good performance of our classifier.
We can also visualize the 32 filters from the first convolutional layer:
visualize.plot_conv_weights(net1.layers_['conv2d1'])
The code above will plot the following filters below:

As you can see, the nolearn plot_conv_weights plots all the filters present in the layer we specified.
Now it is time to create theano-compiled functions that will feed-forward the input data into the architecture up to the layer you’re interested. I’m going to get the functions for the output layer and also for the dense layer before the output layer:
dense_layer = layers.get_output(net1.layers_['dense'], deterministic=True) output_layer = layers.get_output(net1.layers_['output'], deterministic=True) input_var = net1.layers_['input'].input_var f_output = theano.function([input_var], output_layer) f_dense = theano.function([input_var], dense_layer)
As you can see, we have now two theano functions called f_output and f_dense (for the output and dense layers). Please note that in order to get the layers here we are using a extra parameter called “deterministic“, this is to avoid the dropout layers affecting our feed-forward pass.
We can now convert an example instance to the input format and then feed it into the theano function for the output layer:
instance = X_test[0][None, :, :] %timeit -n 500 f_output(instance) 500 loops, best of 3: 858 µs per loop
As you can see, the f_output function takes an average of 858 µs. We can also plot the output layer activations for the instance:
pred = f_output(instance) N = pred.shape[1] plt.bar(range(N), pred.ravel())
The code above will create the following plot:
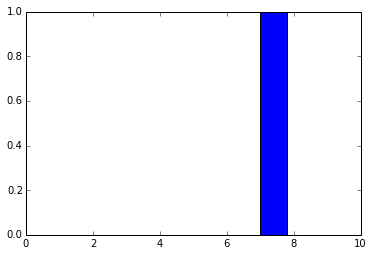
As you can see, the digit was recognized as the digit 7. The fact that you can create theano functions for any layer of the network is very useful because you can create a function (like we did before) to get the activations for the dense layer (the one before the output layer) and you can use these activations as features and use your neural network not as classifier but as a feature extractor. Let’s plot now the 256 unit activations for the dense layer:
pred = f_dense(instance) N = pred.shape[1] plt.bar(range(N), pred.ravel())
The code above will create the following plot below:
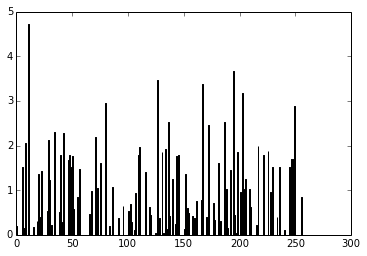
You can now use the output of the these 256 activations as features on a linear classifier like Logistic Regression or SVM.
I hope you enjoyed the tutorial !
Update – 05 Dec 2017: Google just announced that it will be commited to the development of a new released version of the S2 library, amazing news, repository can be found here.
Google’s S2 library is a real treasure, not only due to its capabilities for spatial indexing but also because it is a library that was released more than 4 years ago and it didn’t get the attention it deserved. The S2 library is used by Google itself on Google Maps, MongoDB engine and also by Foursquare, but you’re not going to find any documentation or articles about the library anywhere except for a paper by Foursquare, a Google presentation and the source code comments. You’ll also struggle to find bindings for the library, the official repository has missing Swig files for the Python library and thanks to some forks we can have a partial binding for the Python language (I’m going to it use for this post). I heard that Google is actively working on the library right now and we are probably soon going to get more details about it when they release this work, but I decided to share some examples about the library and the reasons why I think that this library is so cool.
You’ll see this “cell” concept all around the S2 code. The cells are an hierarchical decomposition of the sphere (the Earth on our case, but you’re not limited to it) into compact representations of regions or points. Regions can also be approximated using these same cells, that have some nice features:
The S2 library starts by projecting the points/regions of the sphere into a cube, and each face of the cube has a quad-tree where the sphere point is projected into. After that, some transformation occurs (for more details on why, see the Google presentation) and the space is discretized, after that the cells are enumerated on a Hilbert Curve, and this is why this library is so nice, the Hilbert curve is a space-filling curve that converts multiple dimensions into one dimension that has an special spatial feature: it preserves the locality.

The Hilbert curve is space-filling curve, which means that its range covers the entire n-dimensional space. To understand how this works, you can imagine a long string that is arranged on the space in a special way such that the string passes through each square of the space, thus filling the entire space. To convert a 2D point along to the Hilbert curve, you just need select the point on the string where the point is located. An easy way to understand it is to use this iterative example where you can click on any point of the curve and it will show where in the string the point is located and vice-versa.
In the image below, the point in the very beggining of the Hilbert curve (the string) is located also in the very beginning along curve (the curve is represented by a long string in the bottom of the image):
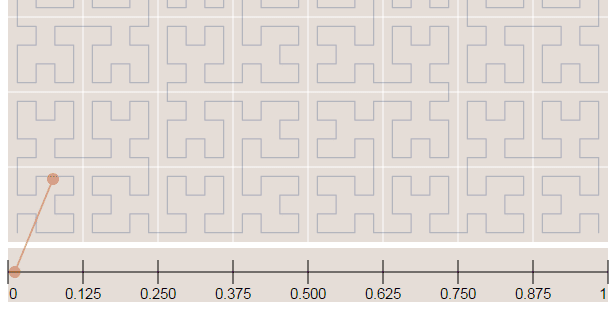
Now in the image below where we have more points, it is easy to see how the Hilbert curve is preserving the spatial locality. You can note that points closer to each other in the curve (in the 1D representation, the line in the bottom) are also closer in the 2D dimensional space (in the x,y plane). However, note that the opposite isn’t quite true because you can have 2D points that are close to each other in the x,y plane that aren’t close in the Hilbert curve.
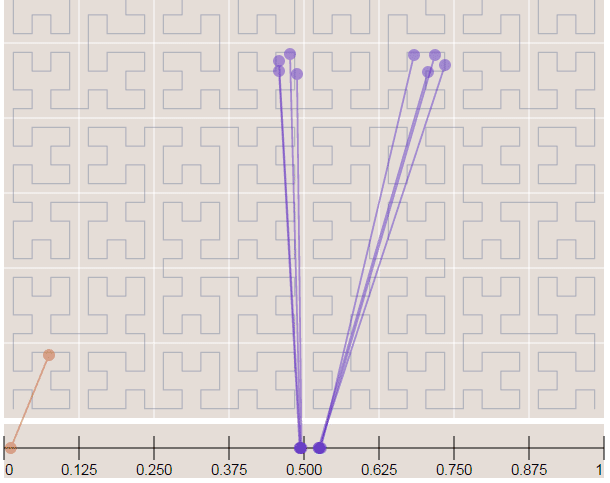
Since S2 uses the Hilbert Curve to enumerate the cells, this means that cell values close in value are also spatially close to each other. When this idea is combined with the hierarchical decomposition, you have a very fast framework for indexing and for query operations. Before we start with the pratical examples, let’s see how the cells are represented in 64-bit integers.
If you are interested in Hilbert Curves, I really recommend this article, it is very intuitive and show some properties of the curve.
As I already mentioned, the cells have different levels and different regions that they can cover. In the S2 library you’ll find 30 levels of hierachical decomposition. The cell level and the area range that they can cover is shown in the Google presentation in the slide that I’m reproducing below:
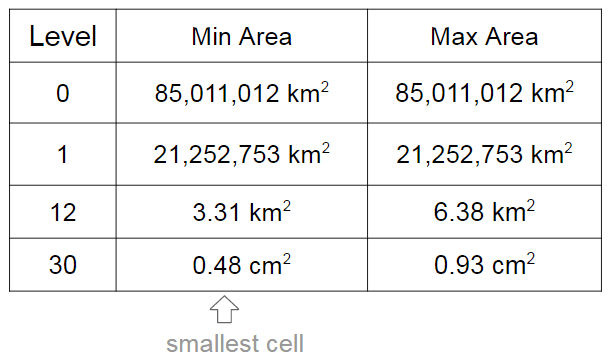
As you can see, a very cool result of the S2 geometry is that every cm² of the earth can be represented using a 64-bit integer.
The cells are represented using the following schema:
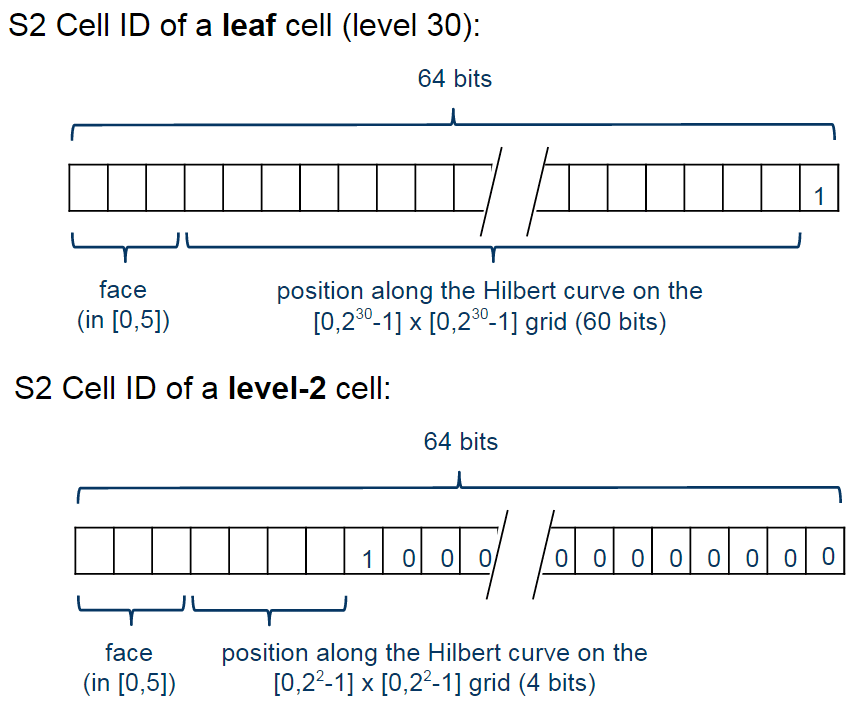
The first one is representing a leaf cell, a cell with the minimum area usually used to represent points. As you can see, the 3 initial bits are reserved to store the face of the cube where the point of the sphere was projected, then it is followed by the position of the cell in the Hilbert curve always followed by a “1” bit that is a marker that will identify the level of the cell.
So, to check the level of the cell, all that is required is to check where the last “1” bit is located in the cell representation. The checking of containment, to verify if a cell is contained in another cell, all you just have to do is to do a prefix comparison. These operations are really fast and they are possible only due to the Hilbert Curve enumeration and the hierarchical decomposition method used.
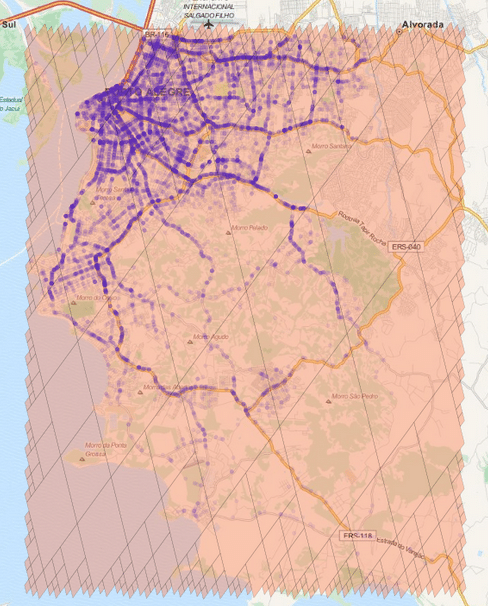
So, if you want to generate cells to cover a region, you can use a method of the library where you specify the maximum number of the cells, the maximum cell level and the minimum cell level to be used and an algorithm will then approximate this region using the specified parameters. In the example below, I’m using the S2 library to extract some Machine Learning binary features using level 15 cells:
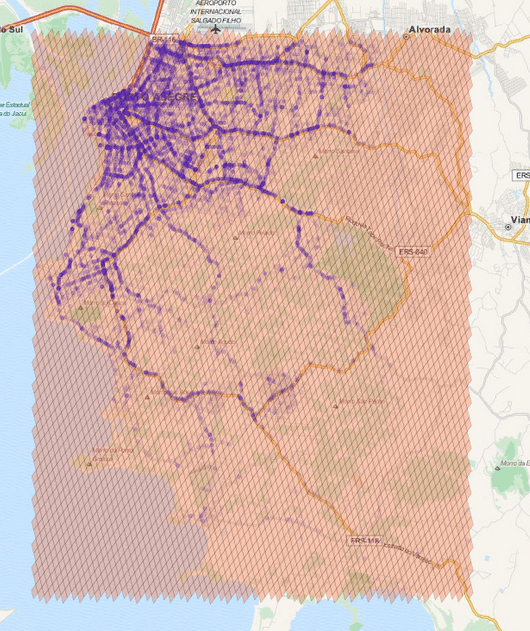
The cells regions are here represented in the image above using transparent polygons over the entire region of interest of my city. Since I used the level 15 both for minimum and maximum level, the cells are all covering similar region areas. If I change the minimum level to 8 (thus allowing the possibility of using larger cells), the algorithm will approximate the region in a way that it will provide the smaller number of cells and also trying to keep the approximation precise like in the example below:
As you can see, we have now a covering using larger cells in the center and to cope with the borders we have an approximation using smaller cells (also note the quad-trees).
* In this tutorial I used the Python 2.7 bindings from the following repository. The instructions to compile and install it are present in the readme of the repository so I won’t repeat it here.
The first step to convert Latitude/Longitude points to the cell representation are shown below:
>>> import s2 >>> latlng = s2.S2LatLng.FromDegrees(-30.043800, -51.140220) >>> cell = s2.S2CellId.FromLatLng(latlng) >>> cell.level() 30 >>> cell.id() 10743750136202470315 >>> cell.ToToken() 951977d377e723ab
As you can see, we first create an object of the class S2LatLng to represent the lat/lng point and then we feed it into the S2CellId class to build the cell representation. After that, we can get the level and id of the class. There is also a method called ToToken that converts the integer representation to a compact alphanumerical representation that you can parse it later using FromToken method.
You can also get the parent cell of that cell (one level above it) and use containment methods to check if a cell is contained by another cell:
>>> parent = cell.parent() >>> print parent.level() 29 >>> parent.id() 10743750136202470316 >>> parent.ToToken() 951977d377e723ac >>> cell.contains(parent) False >>> parent.contains(cell) True
As you can see, the level of the parent is one above the children cell (in our case, a leaf cell). The ids are also very similar except for the level of the cell and the containment checking is really fast (it is only checking the range of the children cells of the parent cell).
These cells can be stored on a database and they will perform quite well on a BTree index. In order to create a collection of cells that will cover a region, you can use the S2RegionCoverer class like in the example below:
>>> region_rect = S2LatLngRect(
S2LatLng.FromDegrees(-51.264871, -30.241701),
S2LatLng.FromDegrees(-51.04618, -30.000003))
>>> coverer = S2RegionCoverer()
>>> coverer.set_min_level(8)
>>> coverer.set_max_level(15)
>>> coverer.set_max_cells(500)
>>> covering = coverer.GetCovering(region_rect)
First of all, we defined a S2LatLngRect which is a rectangle delimiting the region that we want to cover. There are also other classes that you can use (to build polygons for instance), the S2RegionCoverer works with classes that uses the S2Region class as base class. After defining the rectangle, we instantiate the S2RegionCoverer and then set the aforementioned min/max levels and the max number of the cells that we want the approximation to generate.
If you wish to plot the covering, you can use Cartopy, Shapely and matplotlib, like in the example below:
import matplotlib.pyplot as plt
from s2 import *
from shapely.geometry import Polygon
import cartopy.crs as ccrs
import cartopy.io.img_tiles as cimgt
proj = cimgt.MapQuestOSM()
plt.figure(figsize=(20,20), dpi=200)
ax = plt.axes(projection=proj.crs)
ax.add_image(proj, 12)
ax.set_extent([-51.411886, -50.922470,
-30.301314, -29.94364])
region_rect = S2LatLngRect(
S2LatLng.FromDegrees(-51.264871, -30.241701),
S2LatLng.FromDegrees(-51.04618, -30.000003))
coverer = S2RegionCoverer()
coverer.set_min_level(8)
coverer.set_max_level(15)
coverer.set_max_cells(500)
covering = coverer.GetCovering(region_rect)
geoms = []
for cellid in covering:
new_cell = S2Cell(cellid)
vertices = []
for i in xrange(0, 4):
vertex = new_cell.GetVertex(i)
latlng = S2LatLng(vertex)
vertices.append((latlng.lat().degrees(),
latlng.lng().degrees()))
geo = Polygon(vertices)
geoms.append(geo)
print "Total Geometries: {}".format(len(geoms))
ax.add_geometries(geoms, ccrs.PlateCarree(), facecolor='coral',
edgecolor='black', alpha=0.4)
plt.show()
And the result will be the one below:
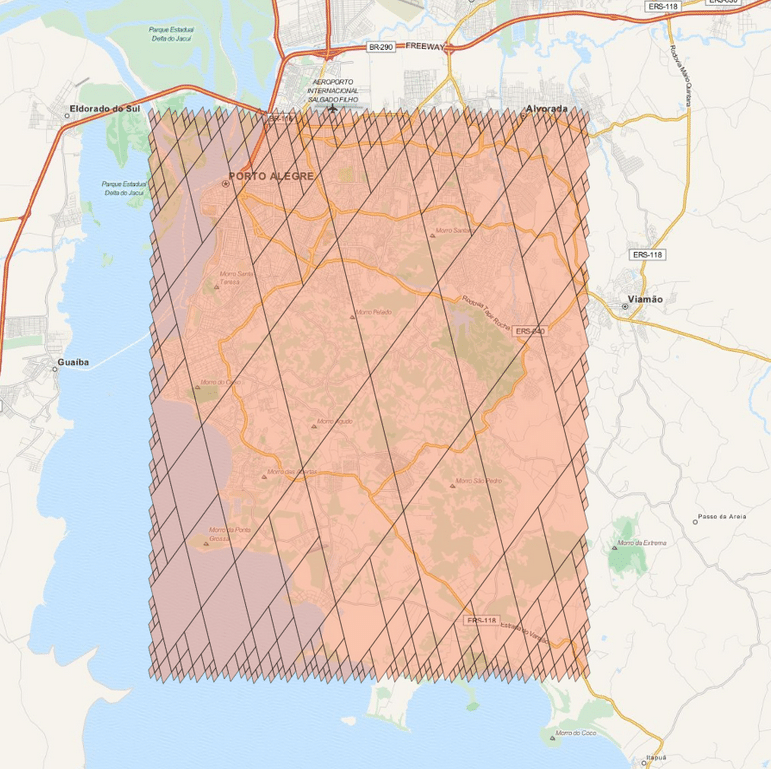
There are a lot of stuff in the S2 API, and I really recommend you to explore and read the source-code, it is really helpful. The S2 cells can be used for indexing and in key-value databases, it can be used on B Trees with really good efficiency and also even for Machine Learning purposes (which is my case), anyway, it is a very useful tool that you should keep in your toolbox. I hope you enjoyed this little tutorial !
– Christian S. Perone
Some time ago I received the Luigi’s Codex Seraphinianus book, for those who still didn’t had a chance to take a look, I really recommend you to buy the book, this is the kind of book that will certainly leave a weirdness in your senses. Codex looks like a treatise of a obscure world, and the Codex alone is by far the most weirdest book I’ve ever seen, so I decided to use the GoogleNet model to create the inceptionisms (using the code based on Caffe, that Google kindly released) with some selected images from the Codex. The result of this process created some very interesting images that I decided to share below (click to enlarge):
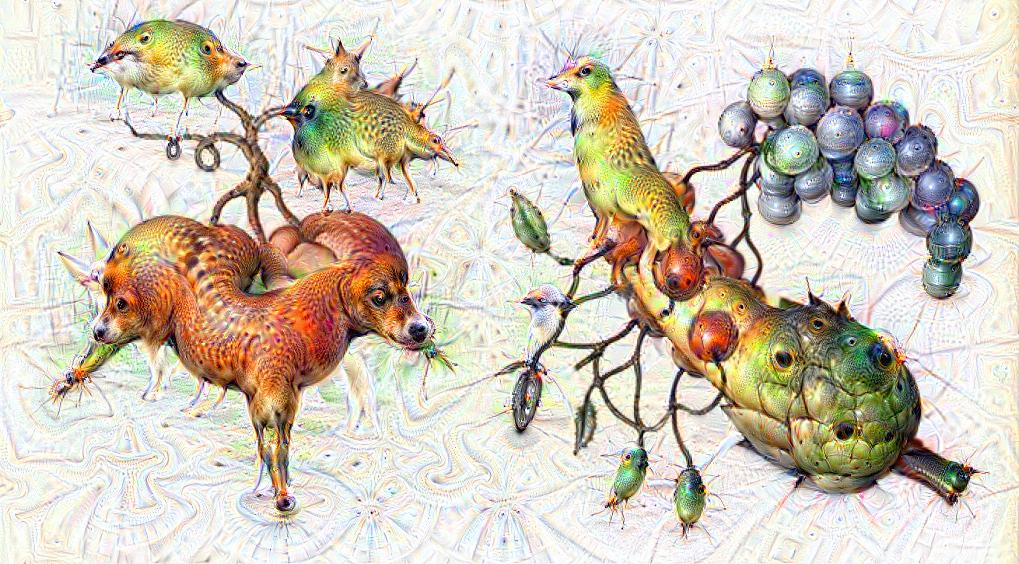
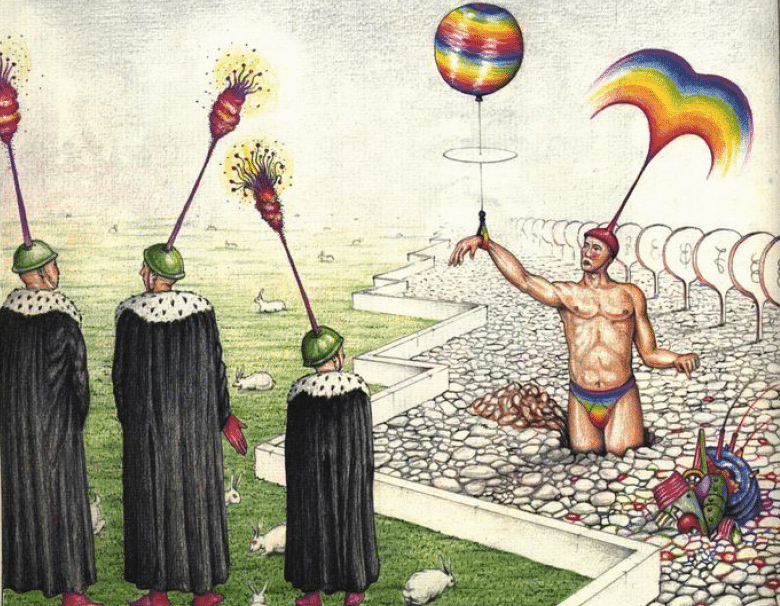

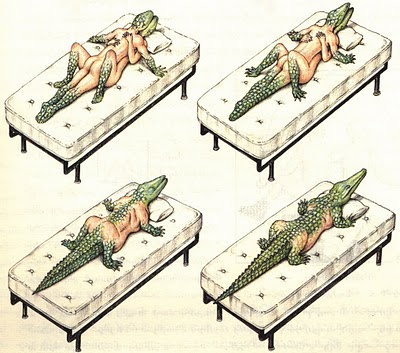



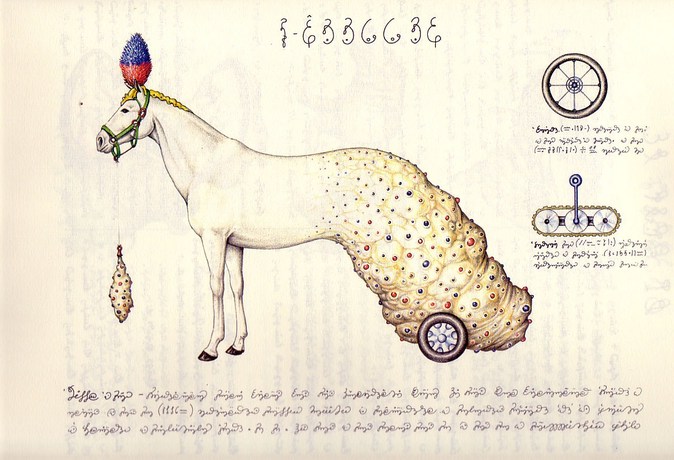
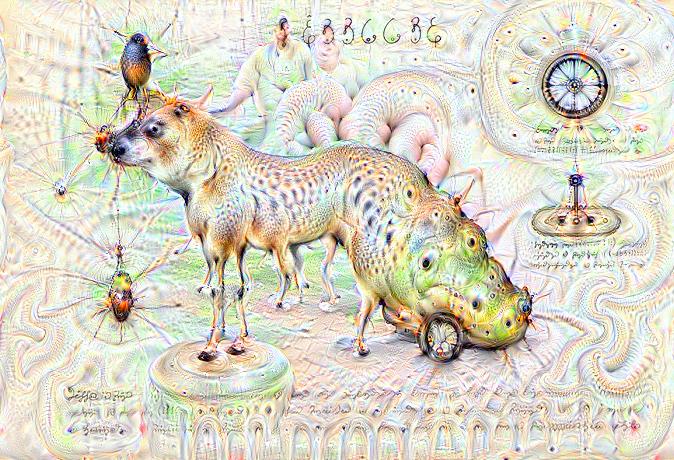
I hope you liked it !
– Christian S. Perone
After flying this past weekend (together with Gabriel and Leandro) with Gabriel’s drone (which is an handmade APM 2.6 based quadcopter) in our town (Porto Alegre, Brasil), I decided to implement a tracking for objects using OpenCV and Python and check how the results would be using simple and fast methods like Meanshift. The result was very impressive and I believe that there is plenty of room for optimization, but the algorithm is now able to run in real time using Python with good results and with a Full HD resolution of 1920×1080 and 30 fps.
Here is the video of the flight that was piloted by Gabriel:
See it in Full HD for more details.
The algorithm can be described as follows and it is very simple (less than 50 lines of Python) and straightforward:
The entire code for the tracking is described below:
import numpy as np
import cv2
def run_main():
cap = cv2.VideoCapture('upabove.mp4')
# Read the first frame of the video
ret, frame = cap.read()
# Set the ROI (Region of Interest). Actually, this is a
# rectangle of the building that we're tracking
c,r,w,h = 900,650,70,70
track_window = (c,r,w,h)
# Create mask and normalized histogram
roi = frame[r:r+h, c:c+w]
hsv_roi = cv2.cvtColor(roi, cv2.COLOR_BGR2HSV)
mask = cv2.inRange(hsv_roi, np.array((0., 30.,32.)), np.array((180.,255.,255.)))
roi_hist = cv2.calcHist([hsv_roi], [0], mask, [180], [0, 180])
cv2.normalize(roi_hist, roi_hist, 0, 255, cv2.NORM_MINMAX)
term_crit = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 80, 1)
while True:
ret, frame = cap.read()
hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
dst = cv2.calcBackProject([hsv], [0], roi_hist, [0,180], 1)
ret, track_window = cv2.meanShift(dst, track_window, term_crit)
x,y,w,h = track_window
cv2.rectangle(frame, (x,y), (x+w,y+h), 255, 2)
cv2.putText(frame, 'Tracked', (x-25,y-10), cv2.FONT_HERSHEY_SIMPLEX,
1, (255,255,255), 2, cv2.CV_AA)
cv2.imshow('Tracking', frame)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
if __name__ == "__main__":
run_main()
I hope you liked it !
I’m working on a new platform (hardware, firmware and software) to create “Stat Cubes“, which are tiny devices with OLED displays and wireless to monitor services or anything you want. While working on it I’ve made a little proof-of-concept using Arduino to monitor Redis server statistics. The Stat Cubes will be open-source in future but I’ve open-sourced the code of the PoC using Arduino and OLED to monitor the Redis server using a Python monitor that sends data from Redis server to the Arduino if someone is interested.
The main idea of Stat Cubes is that you will be able to leave the tiny cubes on your desk or even carry them with you. It will be a long road before I get the first version ready but if people show interest on it I’ll certainly try to speed up things.
Below you can see a video of the display working, you can also visit the repository for more screenshots, information and source-code both for the monitoring application and also for the Arduino code.
See more about the project in the Github repository.


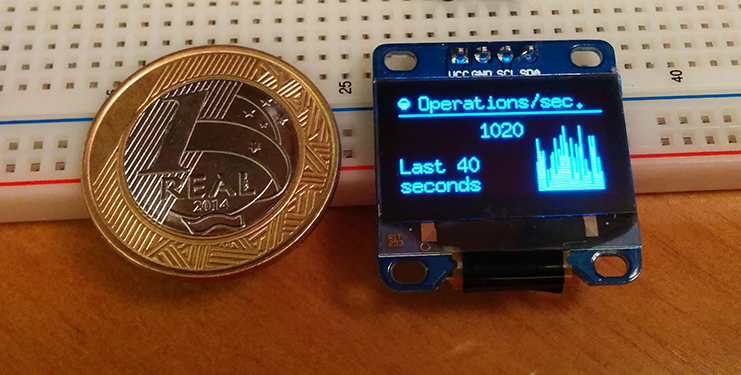

I hope you liked it !
* This post is in portuguese
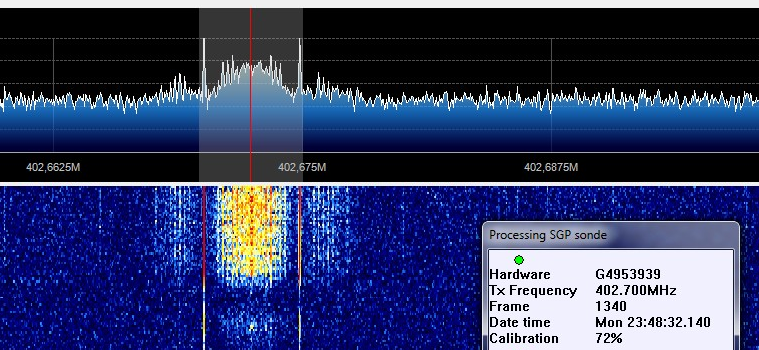
Hoje finalmente consegui rastrear um dos balões meteorológicos que a aeronáutica lança duas vezes por dia aqui em Porto Alegre / RS. A aeronáutica utiliza as sondas da Vaisala (uma empresa finlandesa) modelo RS-92SGP para realizar as medições de umidade, temperatura e pressão. Estes dados são geralmente utilizados para as previsões de tempo da região; existe um datasheet com mais dados sobre o equipamento que eles utilizam, neste datasheet tem informações importantes como por exemplo a frequência em que o aparelho envia os dados de telemetria. Aqui em Porto Alegre / RS a aeronáutica está utilizando a faixa de operação em 402.700Mhz, que também é coberta pelos dongles USB RTLSDR como o que eu utilizo.
O equipamento da Vaisala é um equipamento que utiliza 60mW de potência na transmissão (eu já vi balões transmitindo até 600km nessa frequência com apenas 10mW e com uma antena decente é claro) e utiliza modulação GFSK. Para decodificar o protocolo e GFSK podemos utilizar SDR# juntamente com o Virtual Cable (ou algo semelhante para redirecionar os dados do SDR# para o SondeMonitor que é o software que irá fazer a decodificação dos dados (infelizmente o software é pag e só roda apenas em Windows, mas ao menos vem com alguns dias de trial).
No meu setup eu estou utilizando um dongle RTLSDR R820T juntamente com um Low Noise Amplifier (LNA4ALL na foto abaixo) e uma antena de 5dB omnidirecional:

Abaixo segue a foto do equipamento lançado como payload do balão meteorológico:

Estes balões geralmente atingem uma altitude de uns 20km a 35km, mas isto depende de vários fatores como por exemplo os ventos, a quantidade de gás que foi utilizada no balão, a espessura do latex do balão e outros fatores. Quando o balão estoura este fenômeno é geralmente chamado de “burst” e após este estouro o balão acaba caindo por terra (ele tem uma bateria que não agride a natureza).
Seguem abaixo os screenshots do recebimento dos dados, neste momento eu ainda não havia conseguido receber toda calibração do aparelho:
Screenshot de alguém mais fazendo o tracking da sonda e jogando para o APRS aqui de Porto Alegre:
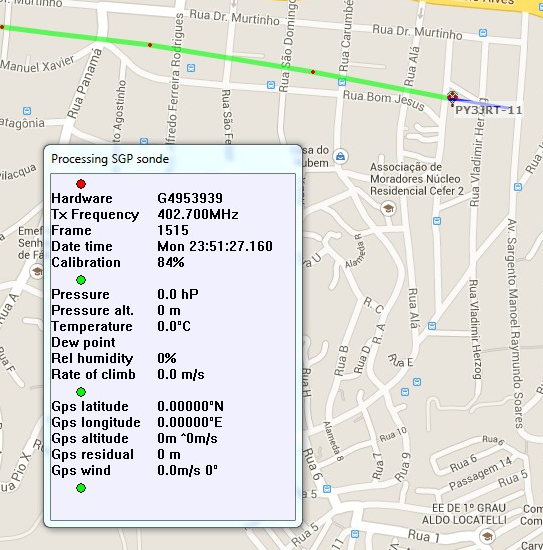
Imagem do rastremento do balão no APRS:
O próximo passo agora é conseguir uma antena direcional para melhorar a recepção =)
Para quem tiver interesse em receber os dados, os balões são lançados diariamente as 00:00 UTC e às 12:00 UTC.
– Christian S. Perone
The new generation of OpenCV bindings for Python is getting better and better with the hard work of the community. The new bindings, called “cv2” are the replacement of the old “cv” bindings; in this new generation of bindings, almost all operations returns now native Python objects or Numpy objects, which is pretty nice since it simplified a lot and also improved performance on some areas due to the fact that you can now also use the optimized operations from Numpy and also enabled the integration with other frameworks like the scikit-image which also uses Numpy arrays for image representation.
In this example, I’ll show how to segment coins present in images or even real-time video capture with a simple approach using thresholding, morphological operators, and contour approximation. This approach is a lot simpler than the approach using Otsu’s thresholding and Watershed segmentation here in OpenCV Python tutorials, which I highly recommend you to read due to its robustness. Unfortunately, the approach using Otsu’s thresholding is highly dependent on an illumination normalization. One could extract small patches of the image to implement something similar to an adaptive Otsu’s binarization (like the one implemented in Letptonica – the framework used by Tesseract OCR) to overcome this problem, but let’s see another approach. For reference, see the output of the Otsu’s thresholding using an image taken with my webcam with a non-normalized illumination:

The first step to create a real-time Video Capture using the Python bindings is to instantiate the VideoCapture class, set the properties and then start reading frames from the camera:
import numpy as np import cv2 cap = cv2.VideoCapture(0) cap.set(cv2.cv.CV_CAP_PROP_FRAME_WIDTH, 1280) cap.set(cv2.cv.CV_CAP_PROP_FRAME_HEIGHT, 720)
In newer versions (unreleased yet), the constants for CV_CAP_PROP_FRAME_WIDTH are now in the cv2 module, for now, let’s just use the cv2.cv module.
The next step is to use the VideoCapture object to read the frames and then convert them to gray color (we are not going to use color information to segment the coins):
while True:
ret, frame = cap.read()
roi = frame[0:500, 0:500]
gray = cv2.cvtColor(roi, cv2.COLOR_BGR2GRAY)
Note that here I’m extracting a small portion of the complete image (where the coins are located), but you don’t have to do that if you have only coins on your image. At this moment, we have the following gray image:

In this step we will apply the Adaptive Thresholding after applying a Gaussian Blur kernel to eliminate the noise that we have in the image:
gray_blur = cv2.GaussianBlur(gray, (15, 15), 0) thresh = cv2.adaptiveThreshold(gray_blur, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY_INV, 11, 1)
See the effect of the Gaussian Kernel in the image:

And now the effect of the Adaptive Thresholding with the blurry image:
Note that at that moment we already have the coins segmented except for the small noisy inside the center of the coins and also in some places around them.
The Morphological Operators are used to dilate, erode and other operations on the pixels of the image. Here, due to the fact that sometimes the camera can present some artifacts, we will use the Morphological Operation of Closing to make sure that the borders of the coins are always close, otherwise, we may found a coin with a semi-circle or something like that. To understand the effect of the Closing operation (which is the operation of erosion of the pixels already dilated) see the image below:
You can see that after some iterations of the operation, the circles start to become filled. To use the Closing operation, we’ll use the morphologyEx function from the OpenCV Python bindings:
kernel = np.ones((3, 3), np.uint8) closing = cv2.morphologyEx(thresh, cv2.MORPH_CLOSE, kernel, iterations=4)
See now the effect of the Closing operation on our coins:
The operations of Morphological Operators are very simple, the main principle is the application of an element (in our case we have a block element of 3×3) into the pixels of the image. If you want to understand it, please see this animation explaining the operation of Erosion.
After applying the morphological operators, all we have to do is to find the contour of each coin and then filter the contours having an area smaller or larger than a coin area. You can imagine the procedure of finding contours in OpenCV as the operation of finding connected components and their boundaries. To do that, we’ll use the OpenCV findContours function.
cont_img = closing.copy() contours, hierarchy = cv2.findContours(cont_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
Note that we made a copy of the closing image because the function findContours will change the image passed as the first parameter, we’re also using the RETR_EXTERNAL flag, which means that the contours returned are only the extreme outer contours. The parameter CHAIN_APPROX_SIMPLE will also return a compact representation of the contour, for more information see here.
After finding the contours, we need to iterate into each one and check the area of them to filter the contours containing an area greater or smaller than the area of a coin. We also need to fit an ellipse to the contour found. We could have done this using the minimum enclosing circle, but since my camera isn’t perfectly above the coins, the coins appear with a small inclination describing an ellipse.
for cnt in contours:
area = cv2.contourArea(cnt)
if area < 2000 or area > 4000:
continue
if len(cnt) < 5:
continue
ellipse = cv2.fitEllipse(cnt)
cv2.ellipse(roi, ellipse, (0,255,0), 2)
Note that in the code above we are iterating on each contour, filtering coins with area smaller than 2000 or greater than 4000 (these are hardcoded values I found for the Brazilian coins at this distance from the camera), later we check for the number of points of the contour because the function fitEllipse needs a number of points greater or equal than 5 and finally we use the ellipse function to draw the ellipse in green over the original image.
To show the final image with the contours we just use the imshow function to show a new window with the image:
cv2.imshow('final result', roi)
And finally, this is the result in the end of all steps described above:

The complete source-code:
import numpy as np
import cv2
def run_main():
cap = cv2.VideoCapture(0)
cap.set(cv2.cv.CV_CAP_PROP_FRAME_WIDTH, 1280)
cap.set(cv2.cv.CV_CAP_PROP_FRAME_HEIGHT, 720)
while(True):
ret, frame = cap.read()
roi = frame[0:500, 0:500]
gray = cv2.cvtColor(roi, cv2.COLOR_BGR2GRAY)
gray_blur = cv2.GaussianBlur(gray, (15, 15), 0)
thresh = cv2.adaptiveThreshold(gray_blur, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY_INV, 11, 1)
kernel = np.ones((3, 3), np.uint8)
closing = cv2.morphologyEx(thresh, cv2.MORPH_CLOSE,
kernel, iterations=4)
cont_img = closing.copy()
contours, hierarchy = cv2.findContours(cont_img, cv2.RETR_EXTERNAL,
cv2.CHAIN_APPROX_SIMPLE)
for cnt in contours:
area = cv2.contourArea(cnt)
if area < 2000 or area > 4000:
continue
if len(cnt) < 5:
continue
ellipse = cv2.fitEllipse(cnt)
cv2.ellipse(roi, ellipse, (0,255,0), 2)
cv2.imshow("Morphological Closing", closing)
cv2.imshow("Adaptive Thresholding", thresh)
cv2.imshow('Contours', roi)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
if __name__ == "__main__":
run_main()