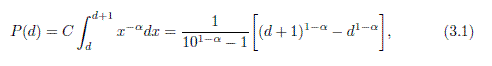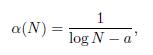This is a simple trick possible using Jython; to call jinja2 template engine under JSP we instantiate the PythonInterpreter class of Jython, set some parameters in the interpreter and then call jinja2 to render a template and write to the Java “out” object.
To install Jython, just download the last stable version Jython 2.5 and then install it as “Standalone” version; the installer will create a simple jython.jar file under the installation directory, copy this package to your Java web project under the \WEB-INF\lib or where you put your web application libraries.
Later, copy the jinja2 module to the \build\classes.
Create a simple template under the WebContent\templates\template.html with contents below:
This is just a Jinja2 template test !
Parameter "p" = {{ request.getParameter("p") }}
Getting session attribute: {{ session.getAttribute("session_attribute") }}
Iterating over Java array:
-
{% for user in users %}
- {{ user }} {% endfor %}
And now create a file called index.jsp in the root of the WebContent, with the contents:
<%@ page language="java" contentType="text/html; charset=ISO-8859-1"
pageEncoding="ISO-8859-1"%>
<%@page import="org.python.util.PythonInterpreter" %>
Jinja2 Template under JSP
<%
PythonInterpreter py = new PythonInterpreter();
String[] users = {"User Number One", "User Number Two"};
session.setAttribute("session_attribute", "Testing Session");
py.set("out", out);
py.set("request", request);
py.set("session", session);
py.set("users", users);
py.set("context_path", application.getRealPath("/") + "templates");
py.exec("from jinja2 import Environment, FileSystemLoader");
py.exec("env = Environment(loader=FileSystemLoader(context_path))");
py.exec("template = env.get_template('template.html')");
py.exec("out.write(template.render(locals()))");
%>
The structure will be like this:
And the output will be something like this: