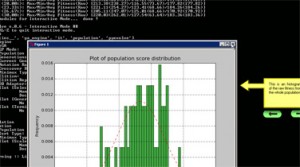
I’ve made a video of an example using the Pyevolve’s Interactive Mode in the middle of the evolution of a Genetic Algorithm. The video is in high resolution, so you can see it here or clicking on the image below:
Sometimes, Benford’s Law is used to check some datasets and detect fraud. If a dataset which is supposed to follow the Benford’s Law distribution diverges from the law, we can say that the dataset is a possible fraud (caution with assumptions, and please, note the word “possible” here).
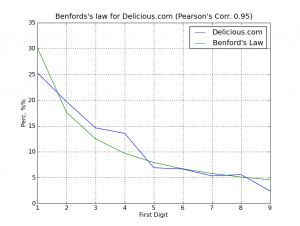
So I had an idea to check the number of users of the Delicious.com website, which is supposed to follow the Benford’s Law. I processed the tag “programming” and I got 40 pages of links with 376 user numbers from links of the Delicious.com. So, here is the plot:
As we can see on the graph, the correlation was 0.95 (between -1 and 1), so we can say (really !!), Delicious.com is not lying about the user numbers on the links =) does anyone knows some suspect sites ?
Follow the source-code of the Python program, it uses a simple regex to get the user numbers from the pages:
import pybenford
import re
import urllib
import time
PAGES = 40
DELICIOUS_URL = "http://delicious.com/tag/programming?page=%d"
reg = re.compile('(\d+)', re.DOTALL | re.IGNORECASE)
users_set = []
for i in xrange(1, PAGES+1):
print "Reading the page %02d of %02d..." % (i, PAGES),
site_handle = urllib.urlopen(DELICIOUS_URL % i)
site_data = site_handle.read()
site_handle.close()
map_to_int = map(int, reg.findall(site_data))
print "%02d records!" % len(map_to_int)
users_set.extend(map_to_int)
time.sleep(5) # Be nice with servers !
print "Total records: %d" % len(users_set)
benford_law = pybenford.benford_law()
digits_scale = pybenford.calc_firstdigit(users_set)
pybenford.plot_comparative(digits_scale, benford_law, "Delicious.com")
UPDATE: See the post “Delicious.com, checking user numbers against Benford’s Law” if you want to see an one more example.
UPDATE 2: Brandon Gray has done a nice related work in Clojure, here is the link to the blog.
As Wikipedia says:
Benford’s law, also called the first-digit law, states that in lists of numbers from many real-life sources of data, the leading digit is distributed in a specific, non-uniform way. According to this law, the first digit is 1 almost one third of the time, and larger digits occur as the leading digit with lower and lower frequency, to the point where 9 as a first digit occurs less than one time in twenty. The basis for this “law” is that the values of real-world measurements are often distributed logarithmically, thus the logarithm of this set of measurements is generally distributed uniformly.
Which means that in a dataset (not all, of course) from a real-life source of data, like for example, the Death Rates, the first digit of every number in this dataset have “1” almost one third of time, “2” in 17.6% of times, and so on in a logarithmic scale. The Benford’s law distribution formulae is:
Where the “n” is the leading digit.
This formulae makes the follow distribution plot (from Wikipedia image):
So I’ve made a Python module, called “pybenford”, which helps me in the creation and analysis of datasets, like the Stock Historical Prices for Apple Inc.
I think that the code is simple enough to understand and reuse:
import pybenford
import csv
def convert_value(value):
return float(value.replace(",","."))
stock_file = open("apple_stock.csv", "r")
csv_apple_stock = csv.reader(stock_file, delimiter=";")
yahoo_format = csv_apple_stock.next()
stock_prices = [ convert_value(row[yahoo_format.index("Volume")]) for row in csv_apple_stock ]
benford_law = pybenford.benford_law()
benford_apple = pybenford.calc_firstdigit(stock_prices)
pybenford.plot_comparative(benford_apple, benford_law, "Apple Stock Volume")
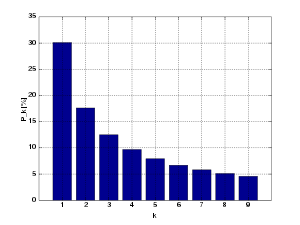
This code will iterate over the Apple Inc. historical data downloaded from Yahoo! Finance and will verify the leading digit for the field “Volume” of the dataset, the dataset is from between 1984 and today (200). Then the pybenford will plot (using Matplotlib) a comparative graph of the dataset with the Benford’s Law distribution. In the graph, there is a Pearson’s Correlation value on the title; the Pearson’s Correlation ranges from +1 to -1. A correlation of +1 means that there is a perfect positive linear relationship between variables.
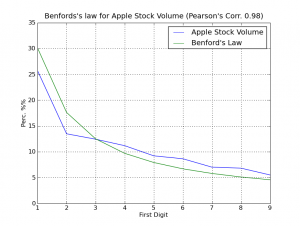
Follow the plot of comparative (click on the image to enlarge):
As you can surprisely see, we have a strong correlation between the Volume data and the Benford’s Law, the Pearson’s Correlation was 0.98, a higher coefficient, this is like black magic for me =)
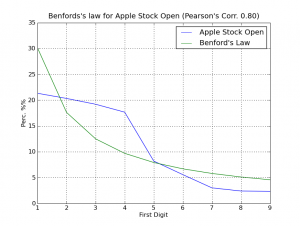
Follow another graph of the opening stock prices:
The correlation this time was low, but it continues with a significant Pearson’s coefficient of 0.80.
I hope you enjoyed =)
The source-code for the “pybenford” can be downloaded here. This module is a simple collection of some very very simple functions.
Hirohisa Aoshima have fixed a bug (an issue on python-twitter when fetching more than 100 users) on Twitter 3D visualization tool and made another video (the blog is in Japanese). Here is the link direct to the video on YouTube.
From the article of LiveScience.com:
The pick and shovel can go only so far in digging up details about dinosaurs. Now supercomputers are revealing knowledge about their anatomy otherwise lost to history.
(…)
For example, if the muscles connected to the thigh bone of a Tyrannosaurus rex were short, that would suggest it was angled vertically as in humans. However, if they were very long, it could have been angled horizontally as in birds.
Initial attempts to randomly decipher which pattern of muscle activation works best result almost always in the animal falling on its face, explained computer paleontologist Peter Falkingham at the University of Manchester. But the scientists employ “genetic algorithms,” or computer programs that can alter themselves and evolve, and so run pattern after pattern until they get improvements.
Eventually, they evolve a pattern of muscle activation with a stable gait and the dinosaur can walk, run, chase or graze, Falkingham said. Assuming natural selection evolves the best possible solution as well, the modeled animal should move similar to its now extinct counterpart. Indeed, they have achieved similar top speeds and gaits with computer versions of humans, emus and ostriches as in reality.
Read the full article.
There is a portuguese version of this post.
Evolutionary computing (EC) has been widely used in recent years, and every year there are new applications for the techniques developed, despite being a relatively new area, few people are giving attention to that (at least in my vision and I will explain why) probably will have a promising and revolutionary future in relation to how we can generate innovation and even learn from it, especially as it relates to Evolutionary Algorithms (EAs).
A Computação Evolutiva (EC) tem sido sido muito utilizada nos últimos anos, e a cada ano que passa, surgem novas aplicações para as técnicas desenvolvidas; apesar de ser uma área relativamente nova, pouca gente está dando a devida atenção ao que (ao menos na minha visão, e vou explicar porque) provavelmente terá um futuro promissor e revolucionário em relação à como podemos gerar a inovação a até mesmo aprender com ela, principalmente no que se relaciona com Algoritmos Evolutivos (EAs).
From the Wired article:
Initially, the equations generated by the program failed to explain the data, but some failures were slightly less wrong than others. Using a genetic algorithm, the program modified the most promising failures, tested them again, chose the best, and repeated the process until a set of equations evolved to describe the systems. Turns out, some of these equations were very familiar: the law of conservation of momentum, and Newton’s second law of motion.
I’m very happy with this news article, I had a similiar idea some time ago, but little different, I’m currently developing it. While in development I always asked myself if it’ll works, but with this good news, maybe it works, but I’ve many work to do yet =)
UPDATE 08/04: you can read the supplemental materials and the report on the Cornell CCSL site.