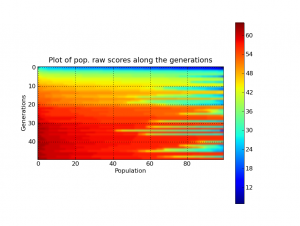
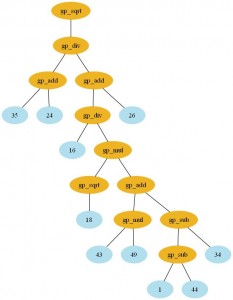
So I did a comparative of Pyevolve GP/GA core in different Python interpreters. I’ve used my Pentium Core 2 Duo (E4500 @ 2.20GHz, 1GB RAM), using Ubuntu 9.04 and Windows XP SP3 just for IronPython 2.6.1 (IronPython doesn’t run with Mono, so I used the win xp with .net 2.0).
The interpreters used were:
I tried using 2009Q3 (the currently main trunk), but I think it’s unstable yet, cause it was more slow than 2009Q2, so I used 2009Q2; I compiled it with GCC 4.3.3 just using the default configure parameters (./configure).
I used the default CPython package of Ubuntu 9.04.
I used the default CPython package of Ubuntu 9.04 too, the python2.5 package.
I used the last svn version of the repository, the release 68612. My Pentium Core 2 Duo had only 1GB of RAM, and the PyPy translation process eats more RAM than Java (sorry for the joke), so I used a notebook with 3GB of RAM to create the pypy-c, what took 1 hour (I used –opt=3) and a beautiful ascii Mandelbrot fractal !
I used the default installer from the Jython project site. I used the Sun JRE 1.6.0_16.
I’ve used the 2.6 RC1 available at IronPython project site with MS .NET 2.0.
To test the GA core I’ve used this source-code (a simple sphere function):
from pyevolve import G1DList
from pyevolve import Mutators, Initializators
from pyevolve import GSimpleGA, Consts
# This is the Sphere Function
def sphere(xlist):
total = 0
for i in xlist:
total += i**2
return total
def run_main():
genome = G1DList.G1DList(140)
genome.setParams(rangemin=-5.12, rangemax=5.13)
genome.initializator.set(Initializators.G1DListInitializatorReal)
genome.mutator.set(Mutators.G1DListMutatorRealGaussian)
genome.evaluator.set(sphere)
ga = GSimpleGA.GSimpleGA(genome, seed=666)
ga.setMinimax(Consts.minimaxType["minimize"])
ga.setGenerations(1500)
ga.setMutationRate(0.01)
ga.evolve(freq_stats=500)
best = ga.bestIndividual()
if __name__ == "__main__":
run_main()
And to test the GP core, I’ve used this source-code (a simple symbolic regression):
from pyevolve import GTree
from pyevolve import Mutators
from pyevolve import GSimpleGA, Consts, Util
import math
rmse_accum = Util.ErrorAccumulator()
def gp_add(a, b): return a+b
def gp_sub(a, b): return a-b
def gp_mul(a, b): return a*b
def gp_sqrt(a): return math.sqrt(abs(a))
def eval_func(chromosome):
global rmse_accum
rmse_accum.reset()
code_comp = chromosome.getCompiledCode()
for a in xrange(0, 10):
for b in xrange(0, 10):
evaluated = eval(code_comp)
target = math.sqrt((a*a)+(b*b))
rmse_accum += (target, evaluated)
return rmse_accum.getRMSE()
def main_run():
genome = GTree.GTreeGP()
genome.setParams(max_depth=4, method="ramped")
genome.evaluator += eval_func
genome.mutator.set(Mutators.GTreeGPMutatorSubtree)
ga = GSimpleGA.GSimpleGA(genome, seed=666)
ga.setParams(gp_terminals = ['a', 'b'],
gp_function_prefix = "gp")
ga.setMinimax(Consts.minimaxType["minimize"])
ga.setGenerations(40)
ga.setCrossoverRate(1.0)
ga.setMutationRate(0.08)
ga.setPopulationSize(800)
ga(freq_stats=10)
best = ga.bestIndividual()
if __name__ == "__main__":
main_run()
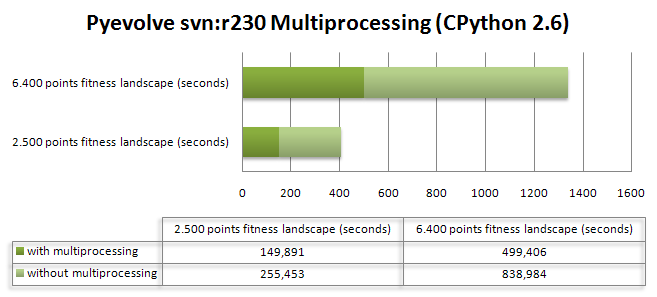
UPDATE 19/08: the x-axis is measured in “seconds“, and the y-axis is the python flavor;
The results are are described in the graph below:
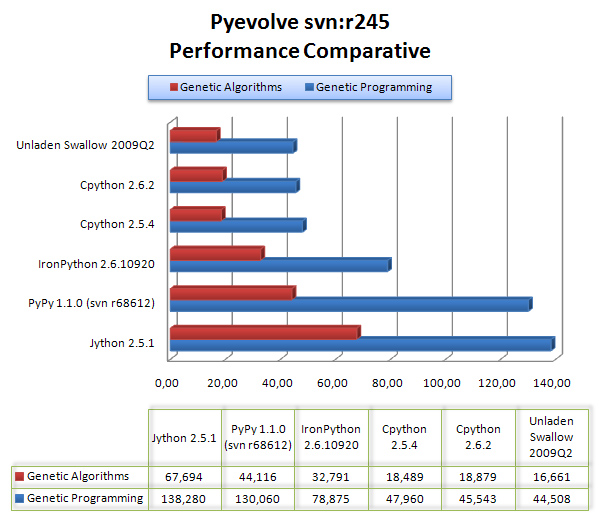As we can see, Unladen Swallow 2009Q2 did a little better performance than CPython 2.6.2, but Jython and PyPy (experimental) were left behind in that scenario, even behind IronPython 2.6.1.
. I’ve used the same seed for the GP, so it has consumed nearly the same cpu resources for both test categories. Here are the results I obtained:
