* It has been a long time since I wrote the TF-IDF tutorial (Part I and Part II) and as I promissed, here is the continuation of the tutorial. Unfortunately I had no time to fix the previous tutorials for the newer versions of the scikit-learn (sklearn) package nor to answer all the questions, but I hope to do that in a close future.
So, on the previous tutorials we learned how a document can be modeled in the Vector Space, how the TF-IDF transformation works and how the TF-IDF is calculated, now what we are going to learn is how to use a well-known similarity measure (Cosine Similarity) to calculate the similarity between different documents.
The Dot Product
Let’s begin with the definition of the dot product for two vectors: and
, where
and
are the components of the vector (features of the document, or TF-IDF values for each word of the document in our example) and the
is the dimension of the vectors:
As you can see, the definition of the dot product is a simple multiplication of each component from the both vectors added together. See an example of a dot product for two vectors with 2 dimensions each (2D):
The first thing you probably noticed is that the result of a dot product between two vectors isn’t another vector but a single value, a scalar.
This is all very simple and easy to understand, but what is a dot product ? What is the intuitive idea behind it ? What does it mean to have a dot product of zero ? To understand it, we need to understand what is the geometric definition of the dot product:
Rearranging the equation to understand it better using the commutative property, we have:
So, what is the term ? This term is the projection of the vector
into the vector
as shown on the image below:
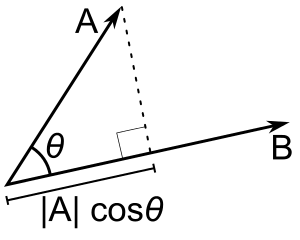
Now, what happens when the vector is orthogonal (with an angle of 90 degrees) to the vector
like on the image below ?
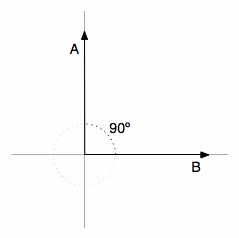
There will be no adjacent side on the triangle, it will be equivalent to zero, the term will be zero and the resulting multiplication with the magnitude of the vector
will also be zero. Now you know that, when the dot product between two different vectors is zero, they are orthogonal to each other (they have an angle of 90 degrees), this is a very neat way to check the orthogonality of different vectors. It is also important to note that we are using 2D examples, but the most amazing fact about it is that we can also calculate angles and similarity between vectors in higher dimensional spaces, and that is why math let us see far than the obvious even when we can’t visualize or imagine what is the angle between two vectors with twelve dimensions for instance.
The Cosine Similarity
The cosine similarity between two vectors (or two documents on the Vector Space) is a measure that calculates the cosine of the angle between them. This metric is a measurement of orientation and not magnitude, it can be seen as a comparison between documents on a normalized space because we’re not taking into the consideration only the magnitude of each word count (tf-idf) of each document, but the angle between the documents. What we have to do to build the cosine similarity equation is to solve the equation of the dot product for the :
And that is it, this is the cosine similarity formula. Cosine Similarity will generate a metric that says how related are two documents by looking at the angle instead of magnitude, like in the examples below:
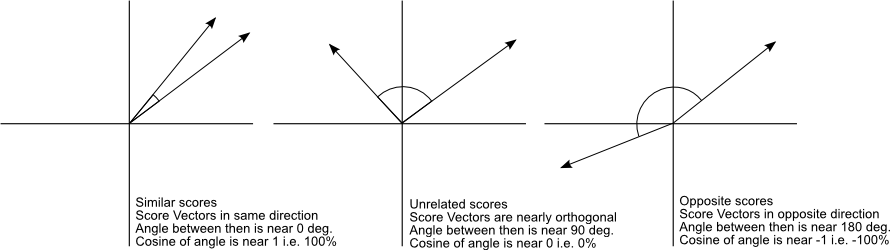
Note that even if we had a vector pointing to a point far from another vector, they still could have an small angle and that is the central point on the use of Cosine Similarity, the measurement tends to ignore the higher term count on documents. Suppose we have a document with the word “sky” appearing 200 times and another document with the word “sky” appearing 50, the Euclidean distance between them will be higher but the angle will still be small because they are pointing to the same direction, which is what matters when we are comparing documents.
Now that we have a Vector Space Model of documents (like on the image below) modeled as vectors (with TF-IDF counts) and also have a formula to calculate the similarity between different documents in this space, let’s see now how we do it in practice using scikit-learn (sklearn).
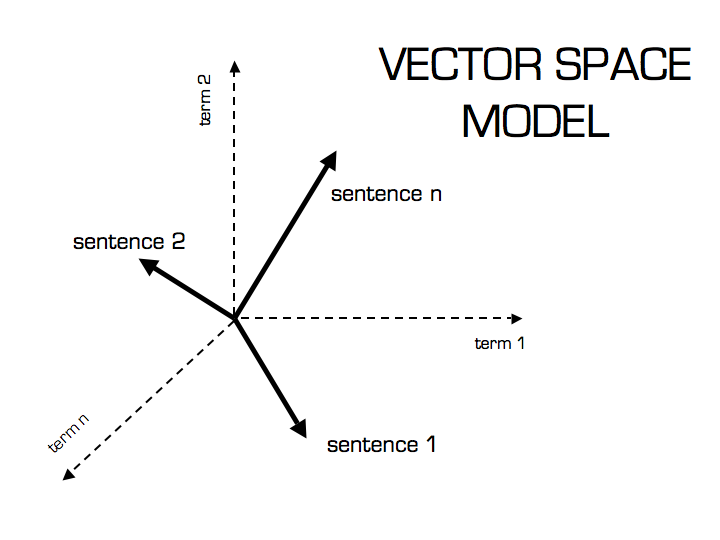
Practice Using Scikit-learn (sklearn)
* In this tutorial I’m using the Python 2.7.5 and Scikit-learn 0.14.1.
The first thing we need to do is to define our set of example documents:
documents = ( "The sky is blue", "The sun is bright", "The sun in the sky is bright", "We can see the shining sun, the bright sun" )
And then we instantiate the Sklearn TF-IDF Vectorizer and transform our documents into the TF-IDF matrix:
from sklearn.feature_extraction.text import TfidfVectorizer tfidf_vectorizer = TfidfVectorizer() tfidf_matrix = tfidf_vectorizer.fit_transform(documents) print tfidf_matrix.shape (4, 11)
Now we have the TF-IDF matrix (tfidf_matrix) for each document (the number of rows of the matrix) with 11 tf-idf terms (the number of columns from the matrix), we can calculate the Cosine Similarity between the first document (“The sky is blue”) with each of the other documents of the set:
from sklearn.metrics.pairwise import cosine_similarity cosine_similarity(tfidf_matrix[0:1], tfidf_matrix) array([[ 1. , 0.36651513, 0.52305744, 0.13448867]])
The tfidf_matrix[0:1] is the Scipy operation to get the first row of the sparse matrix and the resulting array is the Cosine Similarity between the first document with all documents in the set. Note that the first value of the array is 1.0 because it is the Cosine Similarity between the first document with itself. Also note that due to the presence of similar words on the third document (“The sun in the sky is bright”), it achieved a better score.
If you want, you can also solve the Cosine Similarity for the angle between vectors:
We only need to isolate the angle () and move the
to the right hand of the equation:
The is the same as the inverse of the cosine (
).
import math # This was already calculated on the previous step, so we just use the value cos_sim = 0.52305744 angle_in_radians = math.acos(cos_sim) print math.degrees(angle_in_radians) 58.462437107432784
And that angle of ~58.5 is the angle between the first and the third document of our document set.
Related Material
A video about Dot Product on The Khan Academy
Scikit-learn (sklearn) – The de facto Machine Learning package for Python