Hello folks, I always post about Python and EvoComp (Pyevolve), but this time it’s about C, LLVM, search algorithms and data structures. This post describes the efforts to implement an idea: to JIT (verb) algorithms and the data structures used by them, together.

AVL Tree Intro

Here is a short intro to AVL Trees from Wikipedia:

In computer science, an AVL tree is a self-balancing binary search tree, and it is the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; therefore, it is also said to be height-balanced. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

The problem and the idea

When we have a data structure and algorithms to handle (insert, remove and lookup) that structure, the native code of our algorithm is usually full of overhead; for example, in an AVL Tree (Balanced Binary Tree), the overhead appear in: checking if we really have a left or right node while traversing the nodes for lookups, accessing nodes inside nodes, etc. This overhead creates unnecessary assembly operations which in turn, creates native code overhead, even when the compiler optimize it. This overhead directly impacts on the performance of our algorithm (this traditional approach, of course, give us a very flexible structure and the complexity (not Big-O) is easy to handle, but we pay for it: performance loss).

But if you think a little more on how we can improve the lookup performance and how we can remove that overhead from the native code, you’ll discover that we can simply translate the data structure and the algorithm in the native code ITSELF, let me explain it a little better (I will always use the AVL Tree example), when we are looking for a key in an AVL tree, we do something like this (sorry for the GT  – greater than – and LT  – less then -, wordpress messed with the HTML):

lookup_key = 10; // The key we are searching
node = root of the tree;

while True
{
   if (lookup_key == node.key) return node;
   if (lookup_key LT node.key)
   {
      if we don't have a left node, return False;
      else node = node.left_child;
   }

   if (lookup_key GT node.key)
   {
      if we don't have a right node, return False;
      else node = node.right_child;
   }
}

As you can note, this is a generic algorithm for all AVL Tree sizes. Our approach here to remove overhead and JIT the algorithm together with data structure. Let’s make an example, here is the AVL Tree that we’ll convert to code:

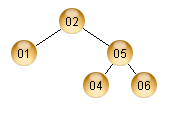
This AVL Tree, when translated to code, can be viewed as something like this:

lookup_key = 10;

if (lookup_key == 2) return 2;
if (lookup_key LT 2)
{
   if (lookup_key == 1) return 1;
   else return -1;

}
if (lookup_key GT 2)
{
   if (lookup_key == 5) return 5;
   if (lookup_key LT 5)
   {
      if (lookup_key == 4) return 4;
      else return -1;
   }
   if (lookup_key GT 5)
   {
      if (lookup_key == 6) return 6;
      else return -1;
   }
}

If you compare this algorithm with the prior one, you’ll note the difference: this algorithm is the algorithm and the data structure itself. It’s something like unrolling the loop of the traditional AVL lookup algorithm.

To codegen an AVL Tree into this code, it’s not very simple as it seems, because to codegen it with LLVM, we must use a a restricted Intermediate Representation (IR), this IR of LLVM uses a RISC-like instruction set, so we must convert this algorithm above into that IR using conditional branching and comparison instructions for later encapsulate it in a function.

The implementation

I’ve used the LLVM 2.6 and the C bindings to implement this algorithm. For the AVL Tree structure, I’ve used the GLib AVL implementation, I’ve used the same structure to do performance comparisons. The LLVM C bindings are not documented, see the notes in the end of this post if you are willing to use them.
The whole source-code is available at SVN Repository.

I implemented the IR codegen in this way:

I first codegen a branch to call when the AVL key we’re looking for doesn’t exist, this branch is called BRNULL, and just returns a -1 integer, meaning that the lookup function haven’t found the key.

Then I add each node of a preorder AVL Tree traversal to a stack, and pop each item to create two branches each: EQ[key], DIF[key]. For example, for the key “1”, I create EQ1 and DIF1, for key 2, I create EQ2 and DIF2, ans so on. Later, when we pop the last item of the stack, we insert a special “entry” branch, which will be the entry point of the function in the IR.

You can see more about this implementation by looking at the source-code of the function called “translate_avl_tree” in the SVN repository.

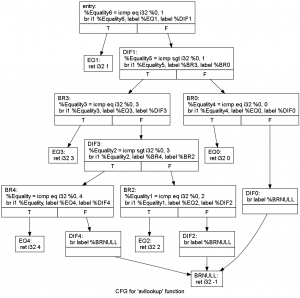
Here is the IR created for an AVL Tree of size 5, the nodes in the AVL are [0,1,2,3,4]:

; ModuleID = ''

define internal i32 @avllookup(i32) {
entry:
  %Equality6 = icmp eq i32 %0, 1                  ;  [#uses=1]
  br i1 %Equality6, label %EQ1, label %DIF1

BRNULL:                                           ; preds = %DIF0, %DIF2, %DIF4
  ret i32 -1

EQ4:                                              ; preds = %BR4
  ret i32 4

DIF4:                                             ; preds = %BR4
  br label %BRNULL

BR4:                                              ; preds = %DIF3
  %Equality = icmp eq i32 %0, 4                   ;  [#uses=1]
  br i1 %Equality, label %EQ4, label %DIF4

EQ2:                                              ; preds = %BR2
  ret i32 2

DIF2:                                             ; preds = %BR2
  br label %BRNULL

BR2:                                              ; preds = %DIF3
  %Equality1 = icmp eq i32 %0, 2                  ;  [#uses=1]
  br i1 %Equality1, label %EQ2, label %DIF2

EQ3:                                              ; preds = %BR3
  ret i32 3

DIF3:                                             ; preds = %BR3
  %Equality2 = icmp sgt i32 %0, 3                 ;  [#uses=1]
  br i1 %Equality2, label %BR4, label %BR2

BR3:                                              ; preds = %DIF1
  %Equality3 = icmp eq i32 %0, 3                  ;  [#uses=1]
  br i1 %Equality3, label %EQ3, label %DIF3

EQ0:                                              ; preds = %BR0
  ret i32 0

DIF0:                                             ; preds = %BR0
  br label %BRNULL

BR0:                                              ; preds = %DIF1
  %Equality4 = icmp eq i32 %0, 0                  ;  [#uses=1]
  br i1 %Equality4, label %EQ0, label %DIF0

EQ1:                                              ; preds = %entry
  ret i32 1

DIF1:                                             ; preds = %entry
  %Equality5 = icmp sgt i32 %0, 1                 ;  [#uses=1]
  br i1 %Equality5, label %BR3, label %BR0

And here is the dot graph of the IR function avllookup created (click to enlarge):

The syntax of the conditional branches in LLVM IR is:

%cond =

icmp

 eq i32 %a, %b
br i1 %cond, label %IfEqual, label %IfUnequal

The “cond” is the condition to jump to another label, if the result of the condition is True, the first label (“IfEqual“) passed as argument for “br” instruction will be the next label to go, otherwise, the label “IfUnequal” will be the next. The “icmp” instruction is the comparison instruction, for more information see the LLVM Assembly Language Reference. In the graph above, the branches are represented as a rectangle with the labels flow directions below (T=True, F = False).

The “ret” is the return instruction, and it syntax is:

ret i32 5

; Return an integer value of 5

Which is self explicative.
This phase of translating the AVL Tree into IR is pretty fast when using the LLVM API, actually, it tooks just 0,64 seconds to codegen a AVL Tree of 10.000 nodes !
After that, I executed the LLVM Transformation Passes over the function created (see the “run_passes” in the source-code), this phase is very fast too, it tooks 0,55 seconds to transform the IR of an AVL Tree of 10.000 nodes (scroll down to see some performance graphs).
After all these phases, we finally do the best part, we JIT the function generated to native code using the LLVM Execution Engine. This phase was, unfortunatelly, the most slow part of JIT’ing the algorithm, for example, it took 4,20 seconds to JIT an AVL Tree with 4.000 nodes. But even with this overhead of compiling the AVL Tree function to native code, I obtained an average of 25% performance over the traditional AVL search algorithm.
Follow the graphs of times spent in each one of the phases, for the JIT compiling and for the comparison between the new method and the traditional AVL search method.
The first graph is a graph of the time spent for JIT’ing different AVL Tree sizes:

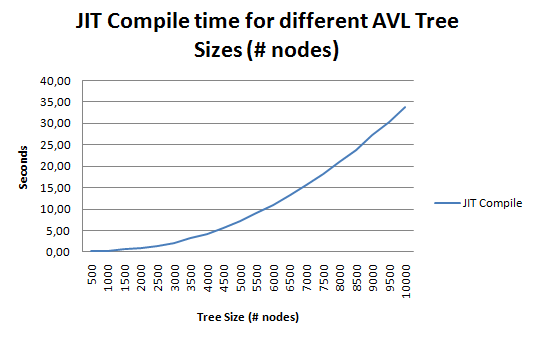
The x-axis is the AVL Tree Size (the number of nodes in the Tree), the y-axis is the time (in seconds) spent to convert that AVL Tree into native code.
The second graph shows the time spent to create the function using the AVL Tree (codegen) and to run optimizations (LLVM Passes):

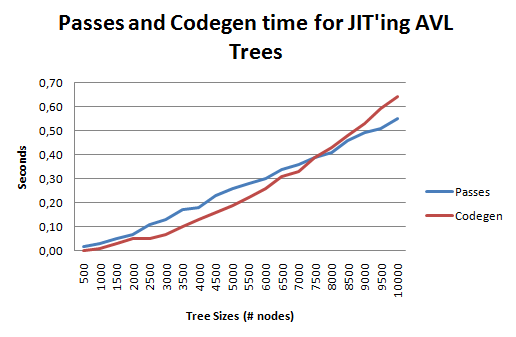
The graph is self-explicative.
And the next graph, is the graph comparing the traditional AVL lookup method vs the JIT’ed AVL Tree lookup:

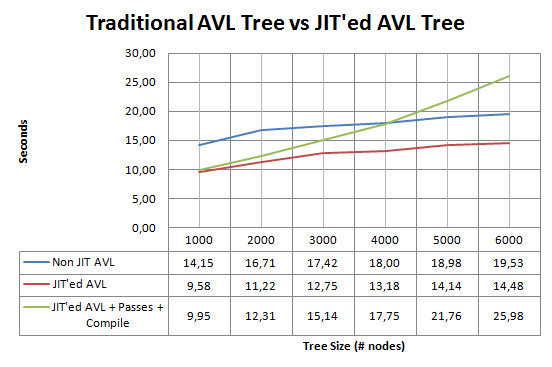
The x-axis is the AVL Tree Size (the number of nodes in the Tree) and the y-axis is the time spent in the lookup of 100000000 random keys.
As you can see, the lookup using the JIT’ed AVL Tree (without the overhead of compiling, running passes, etc) compared to the traditional AVL Tree lookup perform (average) 28% better !
But if we consider the overhead of codegen+passes+JIT’ing the created function, for larger trees (> 4.000) nodes, when the green line (AVL JIT’ed Tree + overhead) crosses the blue line, the overhead of time spent in JIT’ing the function, becomes more slower than the traditional AVL lookup methods.

How code looks like

Take a look at the SVN Repository.

Conclusion

For small AVL Trees (with less than ~3.000 nodes), we can get an average performance of 26% over traditional method, and for AVL Trees with more than 3.000 nodes and less than 4.000 nodes, we can get an average performance of 13%, but with AVL nodes with more than 4.000 nodes, our overhead of compiling that AVL Tree into native code becomes more slower than using the traditional AVL Tree lookup methods.

The successful performance of using this method to JIT search algorithms and data structures, can be very useful when you doesn’t have to JIT it so many times (when you change the AVL Tree), because when we insert or remove nodes from the AVL Tree, it must be reJIT’ed to reflect these changes.
But if you have some CPU idle time, you can adapt a hybrid algorithm to JIT it in this idle time and when you had changed the Tree and you had not yet JIT’ed the new data structure, you can simple use the traditional method, I think that this is the perfect situation for a method like this, because as you can see in the last graph, the red line (new method), when compared with the blue line (traditional method), always have a better performance, near of 30% !!!

Other uses and limitations

This method can be used to JIT other data structures and algorithms, the AVL Tree was just an example of what can be done. I think there are other situations in which we can get more than 30% of performance over traditional methods.
The limitation of this implementation of the AVL Tree was:
1) It uses a fixed data type (Integer) for the key and the value, but you can write a better algorithm to codegen different datatypes;
2) When you change the AVL Tree, you must reJIT it;
3) The memory used is bigger, because you have both the traditional AVL Tree, LLVM IR and the function JIT’ed at same time in memory, maybe there are ways to enhance this;
4) This is just a PoC, what means that the translation algorithm and other parts of the source can be enhanced.

Notes on LLVM

LLVM is very very interesting and useful project, the codegen and transformations are pretty fast ! Unfortunatelly, just the JIT compile is a bit slow for large codes (like a large AVL Tree), but you should note that sometimes, JIT’ing a function just one time is enough to create a better performance, it depends of the dynamics of your problem.
Unfortunatelly, as I cited before, the LLVM C Bindings are not documented, but the code is very clean and you have a good documentation of the LLVM C++ API.
There are some things in which I’ve spent some time:
1) You must call the initialization functions to use the JIT Execution Engine of LLVM, otherwise you’ll get empty error strings (is very hard to find the cause later hehe):

   LLVMLinkInJIT();
   LLVMInitializeNativeTarget();

2) If you set the fastcall convention for a function, like this:

LLVMSetFunctionCallConv(func, LLVMFastCallConv);

You MUST set the attribute “fastcall” using macros in your function pointer:

typedef int (*jit_avl_lookup_t)(int) __attribute__((fastcall));

Otherwise you’ll get very very strange errors, like inserting a “printf” in your code before calling the JIT’ed function, it can change the result of the function return (It’s true!).

I hope you enjoy =)

– Christian S. Perone