vector space model | Terra Incognita

Machine Learning :: Cosine Similarity for Vector Space Models (Part III)

* It has been a long time since I wrote the TF-IDF tutorial (Part I and Part II) and as I promissed, here is the continuation of the tutorial. Unfortunately I had no time to fix the previous tutorials for the newer versions of the scikit-learn (sklearn) package nor to answer all the questions, but I hope to do that in a close future.

So, on the previous tutorials we learned how a document can be modeled in the Vector Space, how the TF-IDF transformation works and how the TF-IDF is calculated, now what we are going to learn is how to use a well-known similarity measure (Cosine Similarity) to calculate the similarity between different documents.

The Dot Product

Let’s begin with the definition of the dot product for two vectors: $\vec{a} = (a_1, a_2, a_3, \ldots)$ and $\vec{b} = (b_1, b_2, b_3, \ldots)$ , where $a_n$ and $b_n$ are the components of the vector (features of the document, or TF-IDF values for each word of the document in our example) and the $\mathit{n}$ is the dimension of the vectors:

$\vec{a} \cdot \vec{b} = \sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n$

As you can see, the definition of the dot product is a simple multiplication of each component from the both vectors added together. See an example of a dot product for two vectors with 2 dimensions each (2D):

$\vec{a} = (0, 3) \\ \vec{b} = (4, 0) \\ \vec{a} \cdot \vec{b} = 0*4 + 3*0 = 0$

The first thing you probably noticed is that the result of a dot product between two vectors isn’t another vector but a single value, a scalar.

This is all very simple and easy to understand, but what is a dot product ? What is the intuitive idea behind it ? What does it mean to have a dot product of zero ? To understand it, we need to understand what is the geometric definition of the dot product:

$\vec{a} \cdot \vec{b} = \|\vec{a}\|\|\vec{b}\|\cos{\theta}$

Rearranging the equation to understand it better using the commutative property, we have:

$\vec{a} \cdot \vec{b} = \|\vec{b}\|\|\vec{a}\|\cos{\theta}$

So, what is the term $\displaystyle \|\vec{a}\|\cos{\theta}$ ? This term is the projection of the vector $\vec{a}$ into the vector $\vec{b}$ as shown on the image below:

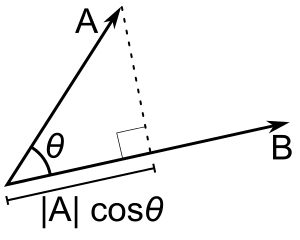
Dot_Product — The projection of the vector A into the vector B. By Wikipedia.

Now, what happens when the vector $\vec{a}$ is orthogonal (with an angle of 90 degrees) to the vector $\vec{b}$ like on the image below ?

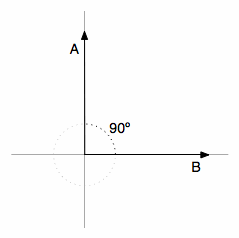
vectors1 — Two orthogonal vectors (with 90 degrees angle).

There will be no adjacent side on the triangle, it will be equivalent to zero, the term $\displaystyle \|\vec{a}\|\cos{\theta}$ will be zero and the resulting multiplication with the magnitude of the vector $\vec{b}$ will also be zero. Now you know that, when the dot product between two different vectors is zero, they are orthogonal to each other (they have an angle of 90 degrees), this is a very neat way to check the orthogonality of different vectors. It is also important to note that we are using 2D examples, but the most amazing fact about it is that we can also calculate angles and similarity between vectors in higher dimensional spaces, and that is why math let us see far than the obvious even when we can’t visualize or imagine what is the angle between two vectors with twelve dimensions for instance.

The Cosine Similarity

The cosine similarity between two vectors (or two documents on the Vector Space) is a measure that calculates the cosine of the angle between them. This metric is a measurement of orientation and not magnitude, it can be seen as a comparison between documents on a normalized space because we’re not taking into the consideration only the magnitude of each word count (tf-idf) of each document, but the angle between the documents. What we have to do to build the cosine similarity equation is to solve the equation of the dot product for the $\cos{\theta}$ :

$\displaystyle \vec{a} \cdot \vec{b} = \|\vec{a}\|\|\vec{b}\|\cos{\theta} \\ \\ \cos{\theta} = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}$

And that is it, this is the cosine similarity formula. Cosine Similarity will generate a metric that says how related are two documents by looking at the angle instead of magnitude, like in the examples below:

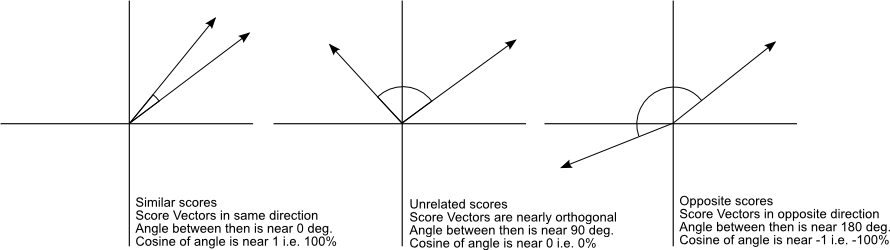
cosinesimilarityfq1 — The Cosine Similarity values for different documents, 1 (same direction), 0 (90 deg.), -1 (opposite directions).

Note that even if we had a vector pointing to a point far from another vector, they still could have an small angle and that is the central point on the use of Cosine Similarity, the measurement tends to ignore the higher term count on documents. Suppose we have a document with the word “sky” appearing 200 times and another document with the word “sky” appearing 50, the Euclidean distance between them will be higher but the angle will still be small because they are pointing to the same direction, which is what matters when we are comparing documents.

Now that we have a Vector Space Model of documents (like on the image below) modeled as vectors (with TF-IDF counts) and also have a formula to calculate the similarity between different documents in this space, let’s see now how we do it in practice using scikit-learn (sklearn).

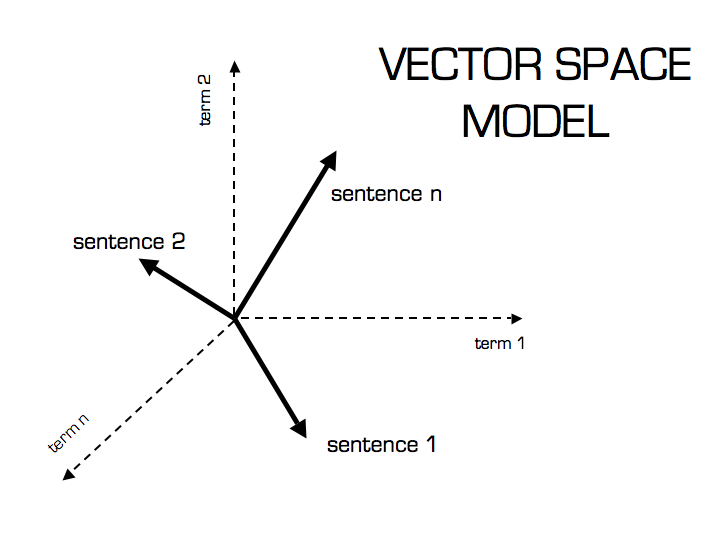
Practice Using Scikit-learn (sklearn)

* In this tutorial I’m using the Python 2.7.5 and Scikit-learn 0.14.1.

The first thing we need to do is to define our set of example documents:

documents = (
"The sky is blue",
"The sun is bright",
"The sun in the sky is bright",
"We can see the shining sun, the bright sun"
)

And then we instantiate the Sklearn TF-IDF Vectorizer and transform our documents into the TF-IDF matrix:

from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(documents)
print tfidf_matrix.shape
(4, 11)

Now we have the TF-IDF matrix (tfidf_matrix) for each document (the number of rows of the matrix) with 11 tf-idf terms (the number of columns from the matrix), we can calculate the Cosine Similarity between the first document (“The sky is blue”) with each of the other documents of the set:

from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(tfidf_matrix[0:1], tfidf_matrix)
array([[ 1.        ,  0.36651513,  0.52305744,  0.13448867]])

The tfidf_matrix[0:1] is the Scipy operation to get the first row of the sparse matrix and the resulting array is the Cosine Similarity between the first document with all documents in the set. Note that the first value of the array is 1.0 because it is the Cosine Similarity between the first document with itself. Also note that due to the presence of similar words on the third document (“The sun in the sky is bright”), it achieved a better score.

If you want, you can also solve the Cosine Similarity for the angle between vectors:

$\cos{\theta} = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}$

We only need to isolate the angle ( $\theta$ ) and move the $\cos$ to the right hand of the equation:

$\theta = \arccos{\frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}}$

The $\arccos$ is the same as the inverse of the cosine ( $\cos^-1$ ).

Lets for instance, check the angle between the first and third documents:

import math
# This was already calculated on the previous step, so we just use the value
cos_sim = 0.52305744
angle_in_radians = math.acos(cos_sim)
print math.degrees(angle_in_radians)
58.462437107432784

And that angle of ~58.5 is the angle between the first and the third document of our document set.

That is it, I hope you liked this third tutorial !

Cite this article as: Christian S. Perone, "Machine Learning :: Cosine Similarity for Vector Space Models (Part III)," in Terra Incognita, 12/09/2013, https://blog.christianperone.com/2013/09/machine-learning-cosine-similarity-for-vector-space-models-part-iii/.

Related Material

A video about Dot Product on The Khan Academy

Wikipedia: Dot Product

Wikipedia: Cosine Similarity

Scikit-learn (sklearn) – The de facto Machine Learning package for Python

12/09/201319/01/2020 by Christian S. Perone

Machine Learning, Python

Machine Learning :: Text feature extraction (tf-idf) – Part I

Short introduction to Vector Space Model (VSM)

In information retrieval or text mining, the term frequency – inverse document frequency (also called tf-idf), is a well know method to evaluate how important is a word in a document. tf-idf are is a very interesting way to convert the textual representation of information into a Vector Space Model (VSM), or into sparse features, we’ll discuss more about it later, but first, let’s try to understand what is tf-idf and the VSM.

VSM has a very confusing past, see for example the paper The most influential paper Gerard Salton Never Wrote that explains the history behind the ghost cited paper which in fact never existed; in sum, VSM is an algebraic model representing textual information as a vector, the components of this vector could represent the importance of a term (tf–idf) or even the absence or presence (Bag of Words) of it in a document; it is important to note that the classical VSM proposed by Salton incorporates local and global parameters/information (in a sense that it uses both the isolated term being analyzed as well the entire collection of documents). VSM, interpreted in a lato sensu, is a space where text is represented as a vector of numbers instead of its original string textual representation; the VSM represents the features extracted from the document.

Let’s try to mathematically define the VSM and tf-idf together with concrete examples, for the concrete examples I’ll be using Python (as well the amazing scikits.learn Python module).

Going to the vector space

The first step in modeling the document into a vector space is to create a dictionary of terms present in documents. To do that, you can simple select all terms from the document and convert it to a dimension in the vector space, but we know that there are some kind of words (stop words) that are present in almost all documents, and what we’re doing is extracting important features from documents, features do identify them among other similar documents, so using terms like “the, is, at, on”, etc.. isn’t going to help us, so in the information extraction, we’ll just ignore them.

Let’s take the documents below to define our (stupid) document space:

Train Document Set:

d1: The sky is blue.
d2: The sun is bright.

Test Document Set:

d3: The sun in the sky is bright.
d4: We can see the shining sun, the bright sun.

Now, what we have to do is to create a index vocabulary (dictionary) of the words of the train document set, using the documents $d1$ and $d2$ from the document set, we’ll have the following index vocabulary denoted as $\mathrm{E}(t)$ where the $t$ is the term:

$\mathrm{E}(t) = \begin{cases} 1, & \mbox{if } t\mbox{ is ``blue''} \\ 2, & \mbox{if } t\mbox{ is ``sun''} \\ 3, & \mbox{if } t\mbox{ is ``bright''} \\ 4, & \mbox{if } t\mbox{ is ``sky''} \\ \end{cases}$

Note that the terms like “is” and “the” were ignored as cited before. Now that we have an index vocabulary, we can convert the test document set into a vector space where each term of the vector is indexed as our index vocabulary, so the first term of the vector represents the “blue” term of our vocabulary, the second represents “sun” and so on. Now, we’re going to use the term-frequency to represent each term in our vector space; the term-frequency is nothing more than a measure of how many times the terms present in our vocabulary $\mathrm{E}(t)$ are present in the documents $d3$ or $d4$ , we define the term-frequency as a couting function:

$\mathrm{tf}(t,d) = \sum\limits_{x\in d} \mathrm{fr}(x, t)$

where the $\mathrm{fr}(x, t)$ is a simple function defined as:

$\mathrm{fr}(x,t) = \begin{cases} 1, & \mbox{if } x = t \\ 0, & \mbox{otherwise} \\ \end{cases}$

So, what the $tf(t,d)$ returns is how many times is the term $t$ is present in the document $d$ . An example of this, could be $tf(``sun'', d4) = 2$ since we have only two occurrences of the term “sun” in the document $d4$ . Now you understood how the term-frequency works, we can go on into the creation of the document vector, which is represented by:

$\displaystyle \vec{v_{d_n}} =(\mathrm{tf}(t_1,d_n), \mathrm{tf}(t_2,d_n), \mathrm{tf}(t_3,d_n), \ldots, \mathrm{tf}(t_n,d_n))$

Each dimension of the document vector is represented by the term of the vocabulary, for example, the $\mathrm{tf}(t_1,d_2)$ represents the frequency-term of the term 1 or $t_1$ (which is our “blue” term of the vocabulary) in the document $d_2$ .

Let’s now show a concrete example of how the documents $d_3$ and $d_4$ are represented as vectors:

$\vec{v_{d_3}} = (\mathrm{tf}(t_1,d_3), \mathrm{tf}(t_2,d_3), \mathrm{tf}(t_3,d_3), \ldots, \mathrm{tf}(t_n,d_3)) \\ \vec{v_{d_4}} = (\mathrm{tf}(t_1,d_4), \mathrm{tf}(t_2,d_4), \mathrm{tf}(t_3,d_4), \ldots, \mathrm{tf}(t_n,d_4))$

which evaluates to:

$\vec{v_{d_3}} = (0, 1, 1, 1) \\ \vec{v_{d_4}} = (0, 2, 1, 0)$

As you can see, since the documents $d_3$ and $d_4$ are:

d3: The sun in the sky is bright.
d4: We can see the shining sun, the bright sun.

The resulting vector $\vec{v_{d_3}}$ shows that we have, in order, 0 occurrences of the term “blue”, 1 occurrence of the term “sun”, and so on. In the $\vec{v_{d_3}}$ , we have 0 occurences of the term “blue”, 2 occurrences of the term “sun”, etc.

But wait, since we have a collection of documents, now represented by vectors, we can represent them as a matrix with $|D| \times F$ shape, where $|D|$ is the cardinality of the document space, or how many documents we have and the $F$ is the number of features, in our case represented by the vocabulary size. An example of the matrix representation of the vectors described above is:

$M_{|D| \times F} = \begin{bmatrix} 0 & 1 & 1 & 1\\ 0 & 2 & 1 & 0 \end{bmatrix}$

As you may have noted, these matrices representing the term frequencies tend to be very sparse (with majority of terms zeroed), and that’s why you’ll see a common representation of these matrix as sparse matrices.

Python practice

Environment Used: Python v.2.7.2, Numpy 1.6.1, Scipy v.0.9.0, Sklearn (Scikits.learn) v.0.9.

Since we know the theory behind the term frequency and the vector space conversion, let’s show how easy is to do that using the amazing scikit.learn Python module.

Scikit.learn comes with lots of examples as well real-life interesting datasets you can use and also some helper functions to download 18k newsgroups posts for instance.

Since we already defined our small train/test dataset before, let’s use them to define the dataset in a way that scikit.learn can use:

train_set = ("The sky is blue.", "The sun is bright.")
test_set = ("The sun in the sky is bright.",
    "We can see the shining sun, the bright sun.")

In scikit.learn, what we have presented as the term-frequency, is called CountVectorizer, so we need to import it and create a news instance:

from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()

The CountVectorizer already uses as default “analyzer” called WordNGramAnalyzer, which is responsible to convert the text to lowercase, accents removal, token extraction, filter stop words, etc… you can see more information by printing the class information:

print vectorizer

CountVectorizer(analyzer__min_n=1,
analyzer__stop_words=set(['all', 'six', 'less', 'being', 'indeed', 'over', 'move', 'anyway', 'four', 'not', 'own', 'through', 'yourselves', (...)

Let’s create now the vocabulary index:

vectorizer.fit_transform(train_set)
print vectorizer.vocabulary
{'blue': 0, 'sun': 1, 'bright': 2, 'sky': 3}

See that the vocabulary created is the same as $E(t)$ (except because it is zero-indexed).

Let’s use the same vectorizer now to create the sparse matrix of our test_set documents:

smatrix = vectorizer.transform(test_set)

print smatrix

(0, 1)        1
(0, 2)        1
(0, 3)        1
(1, 1)        2
(1, 2)        1

Note that the sparse matrix created called smatrix is a Scipy sparse matrix with elements stored in a Coordinate format. But you can convert it into a dense format:

smatrix.todense()

matrix([[0, 1, 1, 1],
........[0, 2, 1, 0]], dtype=int64)

Note that the sparse matrix created is the same matrix $M_{|D| \times F}$ we cited earlier in this post, which represents the two document vectors $\vec{v_{d_3}}$ and $\vec{v_{d_4}}$ .

We’ll see in the next post how we define the idf (inverse document frequency) instead of the simple term-frequency, as well how logarithmic scale is used to adjust the measurement of term frequencies according to its importance, and how we can use it to classify documents using some of the well-know machine learning approaches.

I hope you liked this post, and if you really liked, leave a comment so I’ll able to know if there are enough people interested in these series of posts in Machine Learning topics.

As promised, here is the second part of this tutorial series.

Cite this article as: Christian S. Perone, "Machine Learning :: Text feature extraction (tf-idf) – Part I," in Terra Incognita, 18/09/2011, https://blog.christianperone.com/2011/09/machine-learning-text-feature-extraction-tf-idf-part-i/.

References

The classic Vector Space Model

The most influential paper Gerard Salton never wrote

Wikipedia: tf-idf

Wikipedia: Vector space model

Scikits.learn Examples

Updates

21 Sep 11 – fixed some typos and the vector notation
22 Sep 11 – fixed import of sklearn according to the new 0.9 release and added the environment section
02 Oct 11 – fixed Latex math typos
18 Oct 11 – added link to the second part of the tutorial series
04 Mar 11 – Fixed formatting issues

18/09/201119/01/2020 by Christian S. Perone

Tag: vector space model