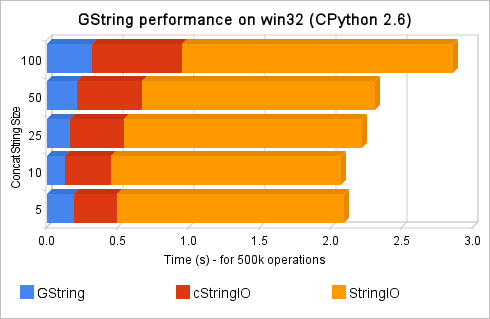
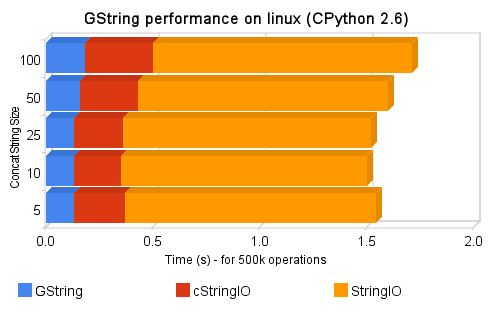
Hello, this is a bridge between Subversion (svn) and Twitter, the intent of this tool is to update a Twitter account when new commit messages arrives in a Subversion repository. We almost never have access to svn repository to add a post-commit hook in a way to call our script and send updates to twitter, so this tool was done to overcome that situation. Using it, you can monitor for example a svn repository from Google Hosting, from Sourceforge.net, etc…
The process of the tool is simple: it will firstly check Twitter account for the last svn commit message (the messages always start with a “$” prefix, or with another user-defined prefix), and then it will check the svn repository server to verify if it has new commits compared to the last tweet revision, if it has, it will update twitter with newer commit messages.
Here is a simple example of a Twitter account updated with commit messages:
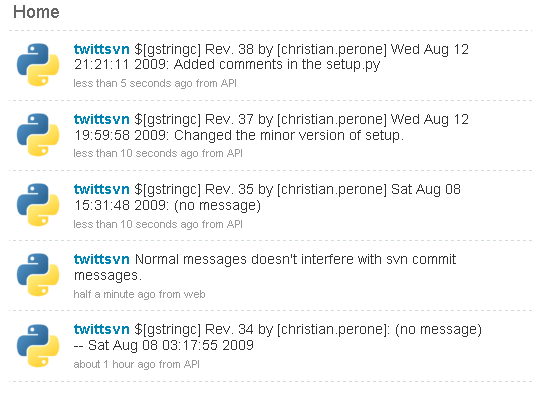
The tool is very simple to use in command-line:
Python twittsvn v.0.1
By Christian S. Perone
https://blog.christianperone.com
Usage: twittsvn.py [options]
Options:
-h, --help show this help message and exit
Twitter Options:
Twitter Accounting Options
-u TWITTER_USERNAME, --username=TWITTER_USERNAME
Twitter username (required).
-p TWITTER_PASSWORD, --password=TWITTER_PASSWORD
Twitter password (required).
-r TWITTER_REPONAME, --reponame=TWITTER_REPONAME
Repository name (required).
-c TWITTER_COUNT, --twittercount=TWITTER_COUNT
How many tweets to fetch from Twitter, default is
'30'.
Subversion Options:
Subversion Options
-s SVN_PATH, --spath=SVN_PATH
Subversion path, default is '.'.
-n SVN_NUMLOG, --numlog=SVN_NUMLOG
Number of SVN logs to get, default is '5'.
And here is a simple example:
# python twittsvn.py -u twitter_username -p twitter_password \
-r any_repository_name
You must execute it in a repository directory (not the server, your local files) or use the “-s” option to specify the path of your local repository. You should put this script to execute periodicaly using cron or something like that.
To use the tool, you must install pysvn and python-twitter. To install Python-twitter you can use “easy_install python-twitter”, but for pysvn you must check the download section at the project site.
Here is the source-code of the twittsvn.py:
# python-twittsvn - A SVN/Twitter bridge
# Copyright (C) 2009 Christian S. Perone
#
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 3 of the License, or
# (at your option) any later version.
#
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
# GNU General Public License for more details.
#
# You should have received a copy of the GNU General Public License
# along with this program. If not, see .
import sys
import re
import time
from optparse import OptionParser, OptionGroup
__version__ = "0.1"
__author__ = "Christian S. Perone "
TWITTER_PREFIX = "$"
TWITTER_MSG = TWITTER_PREFIX + "[%s] Rev. %d by [%s] %s: %s"
try:
import pysvn
except ImportError:
raise ImportError, "pysvn not found, check http://pysvn.tigris.org/project_downloads.html"
try:
import twitter
except ImportError:
raise ImportError, "python-twitter not found, check http://code.google.com/p/python-twitter"
def ssl_server_trust_prompt(trust_dict):
return True, 5, True
def run_main():
parser = OptionParser()
print "Python twittsvn v.%s\nBy %s" % (__version__, __author__)
print "https://blog.christianperone.com\n"
group_twitter = OptionGroup(parser, "Twitter Options",
"Twitter Accounting Options")
group_twitter.add_option("-u", "--username", dest="twitter_username",
help="Twitter username (required).",
type="string")
group_twitter.add_option("-p", "--password", dest="twitter_password",
help="Twitter password (required).",
type="string")
group_twitter.add_option("-r", "--reponame", dest="twitter_reponame",
help="Repository name (required).",
type="string")
group_twitter.add_option("-c", "--twittercount", dest="twitter_count",
help="How many tweets to fetch from Twitter, default is '30'.",
type="int", default=30)
parser.add_option_group(group_twitter)
group_svn = OptionGroup(parser, "Subversion Options",
"Subversion Options")
group_svn.add_option("-s", "--spath", dest="svn_path",
help="Subversion path, default is '.'.",
default=".", type="string")
group_svn.add_option("-n", "--numlog", dest="svn_numlog",
help="Number of SVN logs to get, default is '5'.",
default=5, type="int")
parser.add_option_group(group_svn)
(options, args) = parser.parse_args()
if options.twitter_username is None:
parser.print_help()
print "\nError: you must specify a Twitter username !"
return
if options.twitter_password is None:
parser.print_help()
print "\nError: you must specify a Twitter password !"
return
if options.twitter_reponame is None:
parser.print_help()
print "\nError: you must specify any repository name !"
return
twitter_api = twitter.Api(username=options.twitter_username,
password=options.twitter_password)
twitter_api.SetCache(None) # Dammit cache !
svn_api = pysvn.Client()
svn_api.callback_ssl_server_trust_prompt = ssl_server_trust_prompt
print "Checking Twitter synchronization..."
status_list = twitter_api.GetUserTimeline(options.twitter_username,
count=options.twitter_count)
print "Got %d statuses to check..." % len(status_list)
last_twitter_commit = None
for status in status_list:
if status.text.startswith(TWITTER_PREFIX):
print "SVN Commit messages found !"
last_twitter_commit = status
break
print "Checking SVN logs for ['%s']..." % options.svn_path
log_list = svn_api.log(options.svn_path, limit=options.svn_numlog)
if last_twitter_commit is None:
print "No twitter SVN commit messages found, posting last %d svn commit messages..." % options.svn_numlog
log_list.reverse()
for log in log_list:
message = log["message"].strip()
date = time.ctime(log["date"])
if len(message) <= 0: message = "(no message)"
twitter_api.PostUpdate(TWITTER_MSG % (options.twitter_reponame,
log["revision"].number,
log["author"], date, message))
print "Posted %d svn commit messages to twitter !" % len(log_list)
else:
print "SVN commit messages found in twitter, checking last revision message...."
msg_regex = re.compile(r'Rev\. (\d+) by')
last_rev_twitter = int(msg_regex.findall(last_twitter_commit.text)[0])
print "Last revision detected in twitter is #%d, checking for new svn commit messages..." % last_rev_twitter
rev_num = pysvn.Revision(pysvn.opt_revision_kind.number, last_rev_twitter+1)
try:
log_list = svn_api.log(options.svn_path, revision_end=rev_num,
limit=options.svn_numlog)
except pysvn.ClientError:
print "No more revisions found !"
log_list = []
if len(log_list) <= 0:
print "No new SVN commit messages found !"
print "Updated !"
return
log_list.reverse()
print "Posting new messages to twitter..."
posted_new = 0
for log in log_list:
message = log["message"].strip()
date = time.ctime(log["date"])
if len(message) <= 0:
message = "(no message)"
if log["revision"].number > last_rev_twitter:
twitter_api.PostUpdate(TWITTER_MSG % (options.twitter_reponame,
log["revision"].number,
log["author"], date, message ))
posted_new+=1
print "Posted new %d messages to twitter !" % posted_new
print "Updated!"
if __name__ == "__main__":
run_main()