n-queens problem using Pyevolve
Last night I’ve read a post on Reddit written by Matthew Rollings showing a code in Python to solve Eight Queens puzzle using EA. So I decided to implement it in Python again but this time using Pyevolve, here is the code:
from pyevolve import *
from random import shuffle
BOARD_SIZE = 64
def queens_eval(genome):
collisions = 0
for i in xrange(0, BOARD_SIZE):
if i not in genome: return 0
for i in xrange(0, BOARD_SIZE):
col = False
for j in xrange(0, BOARD_SIZE):
if (i != j) and (abs(i-j) == abs(genome[j]-genome[i])):
col = True
if col == True: collisions +=1
return BOARD_SIZE-collisions
def queens_init(genome, **args):
genome.genomeList = range(0, BOARD_SIZE)
shuffle(genome.genomeList)
def run_main():
genome = G1DList.G1DList(BOARD_SIZE)
genome.setParams(bestrawscore=BOARD_SIZE, rounddecimal=2)
genome.initializator.set(queens_init)
genome.mutator.set(Mutators.G1DListMutatorSwap)
genome.crossover.set(Crossovers.G1DListCrossoverCutCrossfill)
genome.evaluator.set(queens_eval)
ga = GSimpleGA.GSimpleGA(genome)
ga.terminationCriteria.set(GSimpleGA.RawScoreCriteria)
ga.setMinimax(Consts.minimaxType["maximize"])
ga.setPopulationSize(100)
ga.setGenerations(5000)
ga.setMutationRate(0.02)
ga.setCrossoverRate(1.0)
# This DBAdapter is to create graphs later, it'll store statistics in
# a SQLite db file
sqlite_adapter = DBAdapters.DBSQLite(identify="queens")
ga.setDBAdapter(sqlite_adapter)
ga.evolve(freq_stats=10)
best = ga.bestIndividual()
print best
print "\nBest individual score: %.2f\n" % (best.score,)
if __name__ == "__main__":
run_main()
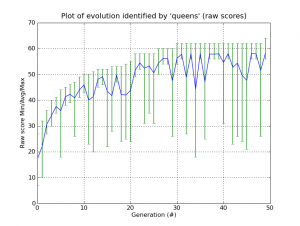
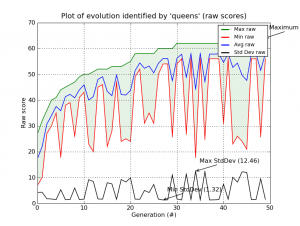
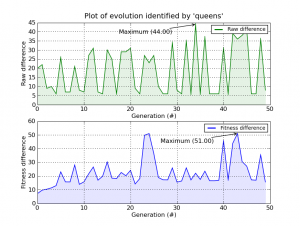
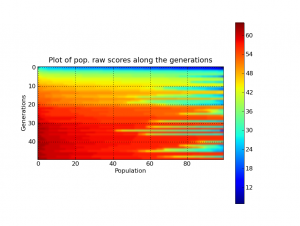
It tooks 49 generations to solve a 64×64 (4.096 chess squares) chessboard, here is the output:
Gen. 0 (0.00%): Max/Min/Avg Fitness(Raw) [20.83(27.00)/13.63(7.00)/17.36(17.36)]
Gen. 10 (0.20%): Max/Min/Avg Fitness(Raw) [55.10(50.00)/39.35(43.00)/45.92(45.92)]
Gen. 20 (0.40%): Max/Min/Avg Fitness(Raw) [52.51(55.00)/28.37(24.00)/43.76(43.76)]
Gen. 30 (0.60%): Max/Min/Avg Fitness(Raw) [67.45(62.00)/51.92(54.00)/56.21(56.21)]
Gen. 40 (0.80%): Max/Min/Avg Fitness(Raw) [65.50(62.00)/19.89(31.00)/54.58(54.58)]
Evolution stopped by Termination Criteria function !
Gen. 49 (0.98%): Max/Min/Avg Fitness(Raw) [69.67(64.00)/54.03(56.00)/58.06(58.06)]
Total time elapsed: 39.141 seconds.
And here is the plots generated by the Graph Plot Tool of Pyevolve:

G1DListCrossoverCutCrossfill undefined?
You must check out the last version in svn repository, these new operators will be part of Pyevolve 0.6, they are not in the version 0.5 (current official version).
Glad my sloppy code could inspire you to write something much neater. I’ve not come across pyevolve before, but it seems very interesting.
One thing I don’t understand is why it takes 39 seconds for your code to complete? is it because you are generating all the information for each generation necessary to make your funky graphs? My program completes in less than 0.1s even with a very low population size.
Mat
Hello Matthew, thanks for the comment; the n-queens you solved was n=8 or n=64 ? The 39 seconds was for the 64×64 board and not for the traditional n=8. The adapter to create graphs has took some time, but they were created after evolution, while the evolution it only stores the data into a sqlite db. There are other issues too, like crossover and mutatation methods, initialization methods, scaling scheme, a non specific problem solving structure, etc…
Ah that’d explain it, my method only does n=8. I shall try my hand at improving my program and solving for n=64 and see how much worse mine is 😉
I think that isn’t “how much worse” and yes “how much better”, you have great chances to get a better performance by doing a specialization in the GA, by not using function slots like I use in Pyevolve into the mutators, crossovers and fitness functions to get a flexible implementation, by not using a scaling method like Linear scaling I’ve used, by not dumping statistics to a SQLite db while evolving, etc… in short, it depends on how close you are to the specialized GA and the problem structure.