October, 2011 | Terra Incognita

Machine Learning, Python

Machine Learning :: Text feature extraction (tf-idf) – Part II

Read the first part of this tutorial: Text feature extraction (tf-idf) – Part I.

This post is a continuation of the first part where we started to learn the theory and practice about text feature extraction and vector space model representation. I really recommend you to read the first part of the post series in order to follow this second post.

Since a lot of people liked the first part of this tutorial, this second part is a little longer than the first.

Introduction

In the first post, we learned how to use the term-frequency to represent textual information in the vector space. However, the main problem with the term-frequency approach is that it scales up frequent terms and scales down rare terms which are empirically more informative than the high frequency terms. The basic intuition is that a term that occurs frequently in many documents is not a good discriminator, and really makes sense (at least in many experimental tests); the important question here is: why would you, in a classification problem for instance, emphasize a term which is almost present in the entire corpus of your documents ?

The tf-idf weight comes to solve this problem. What tf-idf gives is how important is a word to a document in a collection, and that’s why tf-idf incorporates local and global parameters, because it takes in consideration not only the isolated term but also the term within the document collection. What tf-idf then does to solve that problem, is to scale down the frequent terms while scaling up the rare terms; a term that occurs 10 times more than another isn’t 10 times more important than it, that’s why tf-idf uses the logarithmic scale to do that.

But let’s go back to our definition of the $\mathrm{tf}(t,d)$ which is actually the term count of the term $t$ in the document $d$ . The use of this simple term frequency could lead us to problems like keyword spamming, which is when we have a repeated term in a document with the purpose of improving its ranking on an IR (Information Retrieval) system or even create a bias towards long documents, making them look more important than they are just because of the high frequency of the term in the document.

To overcome this problem, the term frequency $\mathrm{tf}(t,d)$ of a document on a vector space is usually also normalized. Let’s see how we normalize this vector.

Vector normalization

Suppose we are going to normalize the term-frequency vector $\vec{v_{d_4}}$ that we have calculated in the first part of this tutorial. The document $d4$ from the first part of this tutorial had this textual representation:

d4: We can see the shining sun, the bright sun.

And the vector space representation using the non-normalized term-frequency of that document was:

$\vec{v_{d_4}} = (0,2,1,0)$

To normalize the vector, is the same as calculating the Unit Vector of the vector, and they are denoted using the “hat” notation: $\hat{v}$ . The definition of the unit vector $\hat{v}$ of a vector $\vec{v}$ is:

$\displaystyle \hat{v} = \frac{\vec{v}}{\|\vec{v}\|_p}$

Where the $\hat{v}$ is the unit vector, or the normalized vector, the $\vec{v}$ is the vector going to be normalized and the $\|\vec{v}\|_p$ is the norm (magnitude, length) of the vector $\vec{v}$ in the $L^p$ space (don’t worry, I’m going to explain it all).

The unit vector is actually nothing more than a normalized version of the vector, is a vector which the length is 1.

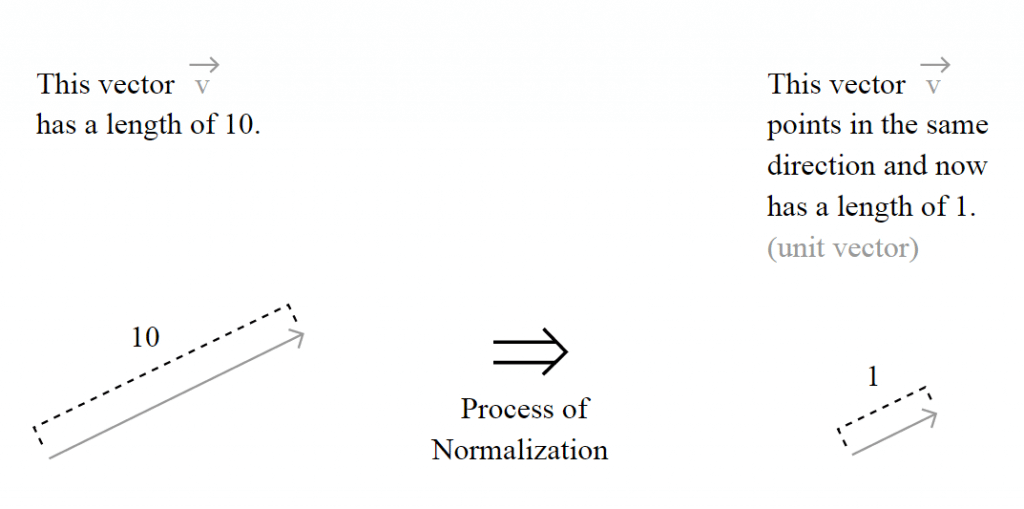
The normalization process (Source: http://processing.org/learning/pvector/)

But the important question here is how the length of the vector is calculated and to understand this, you must understand the motivation of the $L^p$ spaces, also called Lebesgue spaces.

Lebesgue spaces

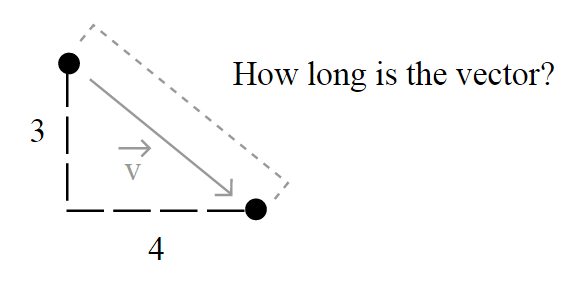
How long is this vector ? (Source: Source: http://processing.org/learning/pvector/)

Usually, the length of a vector $\vec{u} = (u_1, u_2, u_3, \ldots, u_n)$ is calculated using the Euclidean norm – a norm is a function that assigns a strictly positive length or size to all vectors in a vector space -, which is defined by:

(Source: http://processing.org/learning/pvector/)

$\|\vec{u}\| = \sqrt{u^2_1 + u^2_2 + u^2_3 + \ldots + u^2_n}$

But this isn’t the only way to define length, and that’s why you see (sometimes) a number $p$ together with the norm notation, like in $\|\vec{u}\|_p$ . That’s because it could be generalized as:

$\displaystyle \|\vec{u}\|_p = ( \left|u_1\right|^p + \left|u_2\right|^p + \left|u_3\right|^p + \ldots + \left|u_n\right|^p )^\frac{1}{p}$

and simplified as:

$\displaystyle \|\vec{u}\|_p = (\sum\limits_{i=1}^{n}\left|\vec{u}_i\right|^p)^\frac{1}{p}$

So when you read about a L2-norm, you’re reading about the Euclidean norm, a norm with $p=2$ , the most common norm used to measure the length of a vector, typically called “magnitude”; actually, when you have an unqualified length measure (without the $p$ number), you have the L2-norm (Euclidean norm).

When you read about a L1-norm, you’re reading about the norm with $p=1$ , defined as:

$\displaystyle \|\vec{u}\|_1 = ( \left|u_1\right| + \left|u_2\right| + \left|u_3\right| + \ldots + \left|u_n\right|)$

Which is nothing more than a simple sum of the components of the vector, also known as Taxicab distance, also called Manhattan distance.

Taxicab geometry versus Euclidean distance: In taxicab geometry all three pictured lines have the same length (12) for the same route. In Euclidean geometry, the green line has length $6 \times \sqrt{2} \approx 8.48$ , and is the unique shortest path.
Source: Wikipedia :: Taxicab Geometry

Note that you can also use any norm to normalize the vector, but we’re going to use the most common norm, the L2-Norm, which is also the default in the 0.9 release of the scikits.learn. You can also find papers comparing the performance of the two approaches among other methods to normalize the document vector, actually you can use any other method, but you have to be concise, once you’ve used a norm, you have to use it for the whole process directly involving the norm (a unit vector that used a L1-norm isn’t going to have the length 1 if you’re going to take its L2-norm later).

Back to vector normalization

Now that you know what the vector normalization process is, we can try a concrete example, the process of using the L2-norm (we’ll use the right terms now) to normalize our vector $\vec{v_{d_4}} = (0,2,1,0)$ in order to get its unit vector $\hat{v_{d_4}}$ . To do that, we’ll simple plug it into the definition of the unit vector to evaluate it:

$\hat{v} = \frac{\vec{v}}{\|\vec{v}\|_p} \\ \\ \hat{v_{d_4}} = \frac{\vec{v_{d_4}}}{||\vec{v_{d_4}}||_2} \\ \\ \\ \hat{v_{d_4}} = \frac{(0,2,1,0)}{\sqrt{0^2 + 2^2 + 1^2 + 0^2}} \\ \\ \hat{v_{d_4}} = \frac{(0,2,1,0)}{\sqrt{5}} \\ \\ \small \hat{v_{d_4}} = (0.0, 0.89442719, 0.4472136, 0.0)$

And that is it ! Our normalized vector $\hat{v_{d_4}}$ has now a L2-norm $\|\hat{v_{d_4}}\|_2 = 1.0$ .

Note that here we have normalized our term frequency document vector, but later we’re going to do that after the calculation of the tf-idf.

The term frequency – inverse document frequency (tf-idf) weight

Now you have understood how the vector normalization works in theory and practice, let’s continue our tutorial. Suppose you have the following documents in your collection (taken from the first part of tutorial):

Train Document Set:

d1: The sky is blue.
d2: The sun is bright.

Test Document Set:

d3: The sun in the sky is bright.
d4: We can see the shining sun, the bright sun.

Your document space can be defined then as $D = \{ d_1, d_2, \ldots, d_n \}$ where $n$ is the number of documents in your corpus, and in our case as $D_{train} = \{d_1, d_2\}$ and $D_{test} = \{d_3, d_4\}$ . The cardinality of our document space is defined by $\left|{D_{train}}\right| = 2$ and $\left|{D_{test}}\right| = 2$ , since we have only 2 two documents for training and testing, but they obviously don’t need to have the same cardinality.

Let’s see now, how idf (inverse document frequency) is then defined:

$\displaystyle \mathrm{idf}(t) = \log{\frac{\left|D\right|}{1+\left|\{d : t \in d\}\right|}}$

where $\left|\{d : t \in d\}\right|$ is the number of documents where the term $t$ appears, when the term-frequency function satisfies $\mathrm{tf}(t,d) \neq 0$ , we’re only adding 1 into the formula to avoid zero-division.

The formula for the tf-idf is then:

$\mathrm{tf\mbox{-}idf}(t) = \mathrm{tf}(t, d) \times \mathrm{idf}(t)$

and this formula has an important consequence: a high weight of the tf-idf calculation is reached when you have a high term frequency (tf) in the given document (local parameter) and a low document frequency of the term in the whole collection (global parameter).

Now let’s calculate the idf for each feature present in the feature matrix with the term frequency we have calculated in the first tutorial:

$M_{train} = \begin{bmatrix} 0 & 1 & 1 & 1\\ 0 & 2 & 1 & 0 \end{bmatrix}$

Since we have 4 features, we have to calculate $\mathrm{idf}(t_1)$ , $\mathrm{idf}(t_2)$ , $\mathrm{idf}(t_3)$ , $\mathrm{idf}(t_4)$ :

$\mathrm{idf}(t_1) = \log{\frac{\left|D\right|}{1+\left|\{d : t_1 \in d\}\right|}} = \log{\frac{2}{1}} = 0.69314718$

$\mathrm{idf}(t_2) = \log{\frac{\left|D\right|}{1+\left|\{d : t_2 \in d\}\right|}} = \log{\frac{2}{3}} = -0.40546511$

$\mathrm{idf}(t_3) = \log{\frac{\left|D\right|}{1+\left|\{d : t_3 \in d\}\right|}} = \log{\frac{2}{3}} = -0.40546511$

$\mathrm{idf}(t_4) = \log{\frac{\left|D\right|}{1+\left|\{d : t_4 \in d\}\right|}} = \log{\frac{2}{2}} = 0.0$

These idf weights can be represented by a vector as:

$\vec{idf_{train}} = (0.69314718, -0.40546511, -0.40546511, 0.0)$

Now that we have our matrix with the term frequency ( $M_{train}$ ) and the vector representing the idf for each feature of our matrix ( $\vec{idf_{train}}$ ), we can calculate our tf-idf weights. What we have to do is a simple multiplication of each column of the matrix $M_{train}$ with the respective $\vec{idf_{train}}$ vector dimension. To do that, we can create a square diagonal matrix called $M_{idf}$ with both the vertical and horizontal dimensions equal to the vector $\vec{idf_{train}}$ dimension:

$M_{idf} = \begin{bmatrix} 0.69314718 & 0 & 0 & 0\\ 0 & -0.40546511 & 0 & 0\\ 0 & 0 & -0.40546511 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix}$

and then multiply it to the term frequency matrix, so the final result can be defined then as:

$M_{tf\mbox{-}idf} = M_{train} \times M_{idf}$

Please note that the matrix multiplication isn’t commutative, the result of $A \times B$ will be different than the result of the $B \times A$ , and this is why the $M_{idf}$ is on the right side of the multiplication, to accomplish the desired effect of multiplying each idf value to its corresponding feature:

$\begin{bmatrix} \mathrm{tf}(t_1, d_1) & \mathrm{tf}(t_2, d_1) & \mathrm{tf}(t_3, d_1) & \mathrm{tf}(t_4, d_1)\\ \mathrm{tf}(t_1, d_2) & \mathrm{tf}(t_2, d_2) & \mathrm{tf}(t_3, d_2) & \mathrm{tf}(t_4, d_2) \end{bmatrix} \times \begin{bmatrix} \mathrm{idf}(t_1) & 0 & 0 & 0\\ 0 & \mathrm{idf}(t_2) & 0 & 0\\ 0 & 0 & \mathrm{idf}(t_3) & 0\\ 0 & 0 & 0 & \mathrm{idf}(t_4) \end{bmatrix} \\ = \begin{bmatrix} \mathrm{tf}(t_1, d_1) \times \mathrm{idf}(t_1) & \mathrm{tf}(t_2, d_1) \times \mathrm{idf}(t_2) & \mathrm{tf}(t_3, d_1) \times \mathrm{idf}(t_3) & \mathrm{tf}(t_4, d_1) \times \mathrm{idf}(t_4)\\ \mathrm{tf}(t_1, d_2) \times \mathrm{idf}(t_1) & \mathrm{tf}(t_2, d_2) \times \mathrm{idf}(t_2) & \mathrm{tf}(t_3, d_2) \times \mathrm{idf}(t_3) & \mathrm{tf}(t_4, d_2) \times \mathrm{idf}(t_4) \end{bmatrix}$

Let’s see now a concrete example of this multiplication:

$M_{tf\mbox{-}idf} = M_{train} \times M_{idf} = \\ \begin{bmatrix} 0 & 1 & 1 & 1\\ 0 & 2 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} 0.69314718 & 0 & 0 & 0\\ 0 & -0.40546511 & 0 & 0\\ 0 & 0 & -0.40546511 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \\ = \begin{bmatrix} 0 & -0.40546511 & -0.40546511 & 0\\ 0 & -0.81093022 & -0.40546511 & 0 \end{bmatrix}$

And finally, we can apply our L2 normalization process to the $M_{tf\mbox{-}idf}$ matrix. Please note that this normalization is “row-wise” because we’re going to handle each row of the matrix as a separated vector to be normalized, and not the matrix as a whole:

$M_{tf\mbox{-}idf} = \frac{M_{tf\mbox{-}idf}}{\|M_{tf\mbox{-}idf}\|_2}$ $= \begin{bmatrix} 0 & -0.70710678 & -0.70710678 & 0\\ 0 & -0.89442719 & -0.4472136 & 0 \end{bmatrix}$

And that is our pretty normalized tf-idf weight of our testing document set, which is actually a collection of unit vectors. If you take the L2-norm of each row of the matrix, you’ll see that they all have a L2-norm of 1.

Python practice

Environment Used: Python v.2.7.2, Numpy 1.6.1, Scipy v.0.9.0, Sklearn (Scikits.learn) v.0.9.

Now the section you were waiting for ! In this section I’ll use Python to show each step of the tf-idf calculation using the Scikit.learn feature extraction module.

The first step is to create our training and testing document set and computing the term frequency matrix:

from sklearn.feature_extraction.text import CountVectorizer

train_set = ("The sky is blue.", "The sun is bright.")
test_set = ("The sun in the sky is bright.",
"We can see the shining sun, the bright sun.")

count_vectorizer = CountVectorizer()
count_vectorizer.fit_transform(train_set)
print "Vocabulary:", count_vectorizer.vocabulary

# Vocabulary: {'blue': 0, 'sun': 1, 'bright': 2, 'sky': 3}

freq_term_matrix = count_vectorizer.transform(test_set)
print freq_term_matrix.todense()

#[[0 1 1 1]
#[0 2 1 0]]

Now that we have the frequency term matrix (called freq_term_matrix), we can instantiate the TfidfTransformer, which is going to be responsible to calculate the tf-idf weights for our term frequency matrix:

from sklearn.feature_extraction.text import TfidfTransformer

tfidf = TfidfTransformer(norm="l2")
tfidf.fit(freq_term_matrix)

print "IDF:", tfidf.idf_

# IDF: [ 0.69314718 -0.40546511 -0.40546511  0.        ]

Note that I’ve specified the norm as L2, this is optional (actually the default is L2-norm), but I’ve added the parameter to make it explicit to you that it it’s going to use the L2-norm. Also note that you can see the calculated idf weight by accessing the internal attribute called idf_. Now that fit() method has calculated the idf for the matrix, let’s transform the freq_term_matrix to the tf-idf weight matrix:

tf_idf_matrix = tfidf.transform(freq_term_matrix)
print tf_idf_matrix.todense()

# [[ 0.         -0.70710678 -0.70710678  0.        ]
# [ 0.         -0.89442719 -0.4472136   0.        ]]

And that is it, the tf_idf_matrix is actually our previous $M_{tf\mbox{-}idf}$ matrix. You can accomplish the same effect by using the Vectorizer class of the Scikit.learn which is a vectorizer that automatically combines the CountVectorizer and the TfidfTransformer to you. See this example to know how to use it for the text classification process.

I really hope you liked the post, I tried to make it simple as possible even for people without the required mathematical background of linear algebra, etc. In the next Machine Learning post I’m expecting to show how you can use the tf-idf to calculate the cosine similarity.

If you liked it, feel free to comment and make suggestions, corrections, etc.

Cite this article as: Christian S. Perone, "Machine Learning :: Text feature extraction (tf-idf) – Part II," in Terra Incognita, 03/10/2011, https://blog.christianperone.com/2011/10/machine-learning-text-feature-extraction-tf-idf-part-ii/.