Machine Learning

Diffusion Elites: surprisingly good, simple and embarrassingly parallel

Introduction

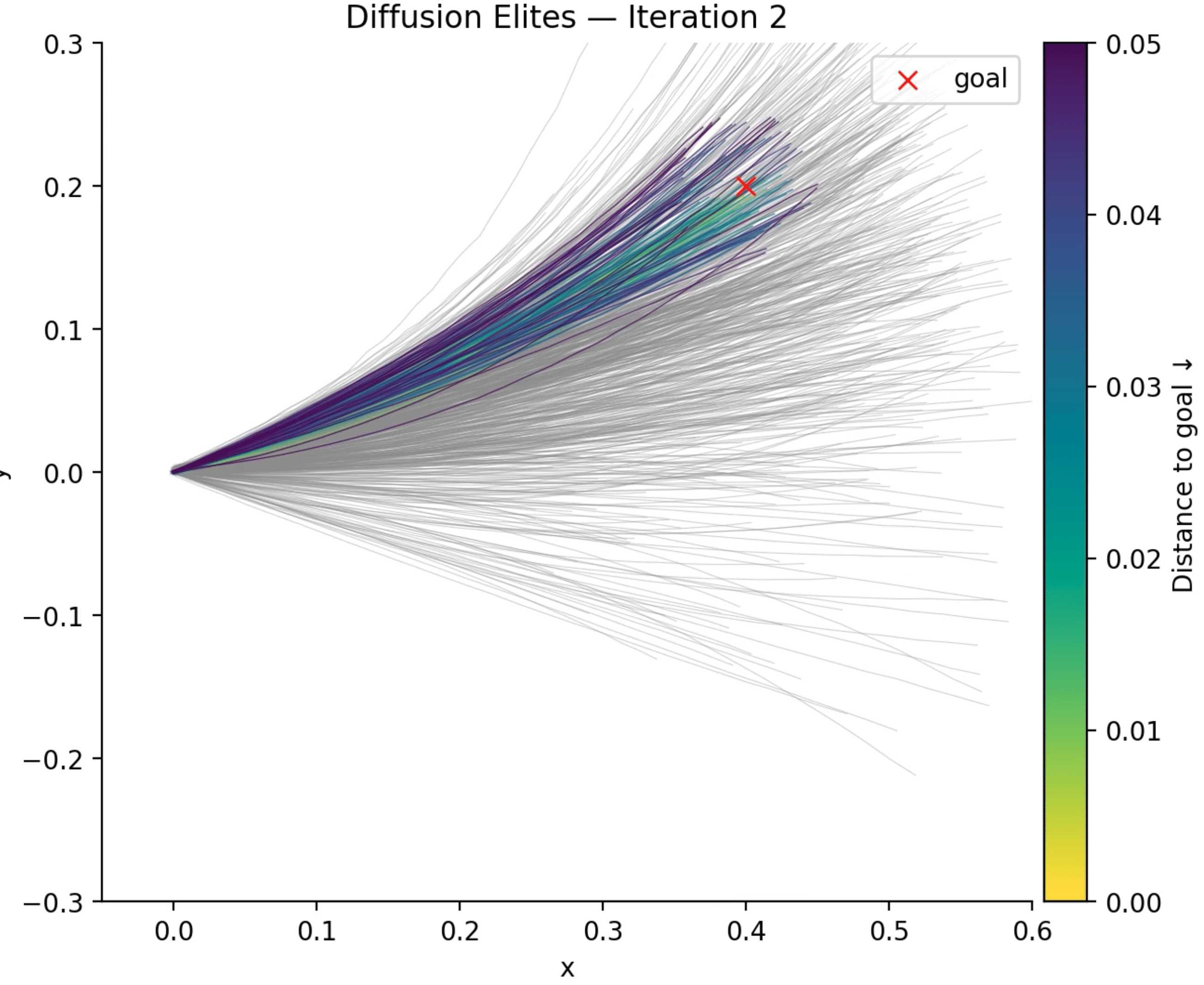It is not a secret that Diffusion models have become the workhorses of high-dimensionality generation: start with a Gaussian noise and, through a learned denoising trajectory, you get high-fidelity images, molecular graphs, or robot trajectories that look (uncannily) real. I wrote extensively about diffusion and its connection with the data manifold metric tensor recently as well, so if you are interested please take a look on it.

Now, for many engineering and practical tasks we care less about “looking real” and more about maximising a task-specific score or a reward from a simulator, a chemistry docking metric, a CLIP consistency score, human preference, etc. Even though we can use guidance or do a constrained sampling from the model, we often require differentiable functions for that. Evolution-style search methods (CEM, CMA-ES, etc), however, can shine in that regime, but naively applying them in the raw object space wastes most samples on absurd or invalid candidates and takes a lot of time to converge to a reasonable solution.

I have been experimenting on some personal projects with something that we can call “Diffusion Elites“, which aims to close this gap by letting a pre-trained diffusion model provide the prior and letting an adapted Cross-Entropy Method (CEM) steer the search inside its latent space instead. I found that this works quite well for many domains and it is also an impressively flexible method with a lot to explore (I will talk about some cases later).

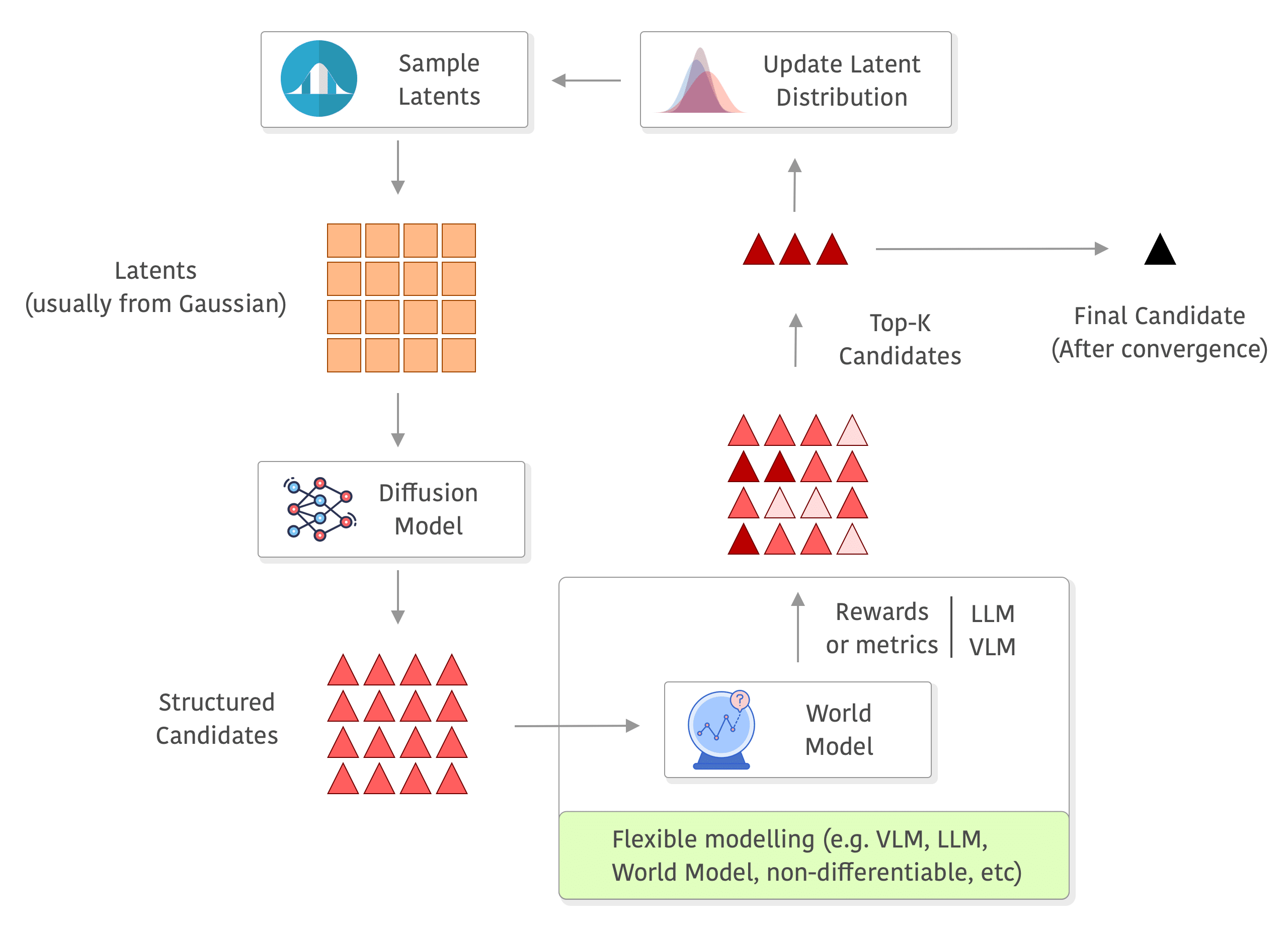
To summarize, the method is as simple as the following:

Draw a population of latent vectors from a Gaussian
Run one full denoise pass to turn each latent into a structured object
Score every object with any reward function
Keep the top-K “elite” latents, refit a new Gaussian to them, and iterate

This five-line loop inherits the robust, gradient-free advantages of evolutionary search while guaranteeing that every candidate lives on the diffusion model’s data manifold. In practice that means fewer wasted evaluations, faster convergence, and dramatically higher-quality solutions for many tasks (e.g. planning, design, etc). In the rest of this post I will unpack the Diffusion Elites in detail, from the algorithm to some coding examples. Diffusion Elites shows that you can explore a diffusion model and turn it into a powerful black box optimizer, it is like doing search on the data manifold itself.

Diffusion Elites

Overview diagram

Below you can see a diagram of the process, I added a world model in the rewards to exemplify how you can use a world model and even do roll-outs there without any differentiability requirements, but you can really use anything to compute your rewards (e.g. you can also compute metrics on the outputs of the world model, or use a VLM/LLM as judge or even as world model as well):

(more…)

09/07/202521/07/2025 by Christian S. Perone

Machine Learning

TorchStation Prototype V1 – GPUs panel

I finally had some time over the holidays to complete the first panel of the TorchStation. The core idea is to have a monitor box that sits on your desk and tracks distributed model training. The panel shown below is a prototype for displaying GPU usage and memory. I’ll continue to post updates as I add more components. The main challenge with this board was power: the LED bars alone drew around 1.2A (when all full brightness and all lit up), so I had to use an external power supply and do a common ground with the MCU, for the panel I used a PLA Matte and 3mm. Wiring was the worst, this panel alone required at least 32 wires, but the panel will hide it quite well. I’m planning to support up to 8 GPUs per node, which aligns with the typical maximum found in many cloud instances. Here is the video, which was quite tricky to capture because of the camera metering of exposure that kept changing due to the LEDs (the video doesn’t do justice to how cool these LEDs are, they are very bright and clear even in daylight):

I’m using for the interface the Arduino Mega (which uses the ATmega2560) and Grove ports to make it easier to connect all of this, but I had to remove all VCCs from the ports to be able to supply from an external power supply, in the end it looks like this below:

                 ┌────────── PC USB (5V, ≤500 mA)
                 │
            +5 V │
                 ▼
     ┌─────────────────┐
     │  Arduino Mega   │  Data pins D2…D13, D66…D71 → LED bars
     └─────────────────┘
                ▲  GND (common reference)
                │
   ┌────────────┴──────────────┐
   │ 5V, ≥3 A switching PSU    │  ← external PSU
   └───────┬───────────┬───────┘
           │           │
           │ +5V       │ GND
           ▼           ▼
┌─────────────────────────────────┐
│ Grove Ports (VCC rail)          │ <– external 5V injected here
│ 8 × LED Bar cables              │
└─────────────────────────────────┘

28/05/202528/05/2025 by Christian S. Perone

Machine Learning

Large language model data pipelines and Common Crawl (WARC/WAT/WET)

Erik Desmazieres’s “La Bibliothèque de Babel”. 1997.

We have been training language models (LMs) for years, but finding valuable resources about the data pipelines commonly used to build the datasets for training these models is paradoxically challenging. It may be because we often take it for granted that these datasets exist (or at least existed? As replicating them is becoming increasingly difficult). However, one must consider the numerous decisions involved in creating such pipelines, as it can significantly impact the final model’s quality, as seen recently in the struggle of models aiming to replicate LLaMA (LLaMA: Open and Efficient Foundation Language Models). It might be tempting to think that now, with large models that can scale well, data is becoming more critical than modeling, since model architectures are not radically changing much. However, data has always been critical.

This article provides a short introduction to the pipeline used to create the data to train LLaMA, but it allows for many variations and I will add details about other similar pipelines when relevant, such as RefinedWeb (The RefinedWeb Dataset for Falcon LLM: Outperforming Curated Corpora with Web Data, and Web Data Only) and The Pile (The Pile: An 800GB Dataset of Diverse Text for Language Modeling). This article is mainly based on the pipeline described in CCNet (CCNet: Extracting High Quality Monolingual Datasets from Web Crawl Data) and LLaMA’s paper, both from Meta. CCNet was developed focusing on the data source that is often the largest one, but also the most challenging in terms of quality: Common Crawl.

The big picture

The entire pipeline of CCNet (plus some minor modifications made by LLaMA’s paper) can be seen below. It has the following stages: data source, deduplication, language, filtering, and the “is-reference” filtering which was added in LLaMA. I will go through each one of them in the sections below.

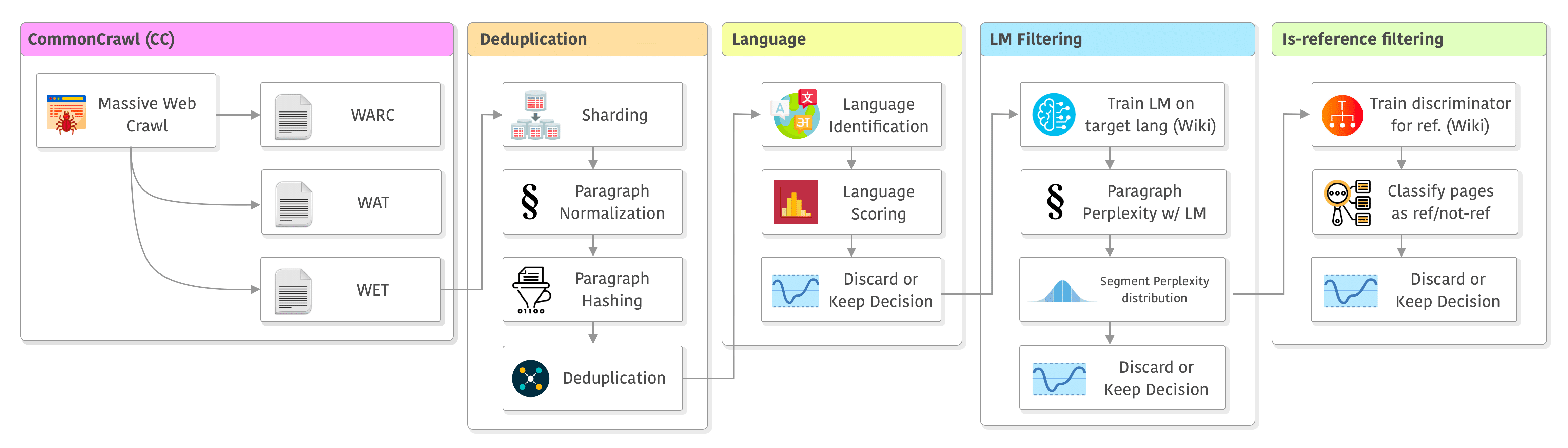
*Visual overview of the CCNet pipeline with some modifications done in LLaMA. Click to enlarge*.

Let’s dive into it !

(more…)

03/06/202304/06/2023 by Christian S. Perone

Uncategorized

PyTorch 2 Internals – Talk

Just sharing ~100 slides about PyTorch 2 internals focusing on recent innovations (Dynamo, Inductor, and ExecuTorch). I had a lot of fun preparing this and hope you’ll enjoy it. I’m planning to record it soon.

Download link for the slides are here.
Slides in SlideShare are here.

(more…)

11/12/202329/01/2024 by Christian S. Perone

Machine Learning, Programming

Torch Titan distributed training code analysis

I really like to peek into different ML codebases for distributed training and this is a very short post on some things I found interesting in Torch Titan:

Disable and control of Python’s garbage collector (GC): titan codebase disables the Python GC and then manually forces a collection in the beginning of every training step during the training loop. This makes sense, but I’m not sure what are the gains of doing it, I think doing every step can be too much and I’m not sure if taking control of GC would be worth for the gains you get by manually controlling it, especially depending on complexity of other dependencies you use, as this could cause unintended behavior that would be difficult to associate with the GC collection;

Custom GPU memory monitoring: titan has a custom class to monitor GPU memory that is quite nice, it resets peak stats and empty the CUDA caching allocator upon initialization. At every step then they collect the peak stats for both small and large pools by capturing the stats for active, reserved and also failed retries and number of OOMs. It is very common for people to just monitor max GPU usage externally from NVML, however, this ignores the fact that PyTorch uses a caching allocator and that you need to look at the internal memory management mechanism inside PyTorch. If you don’t do that, you will certainly be mislead by what you are getting from NVML;

Custom profiling context manager: they wrote a context manager for profiling, where they measure time it takes to dump the profiling data per rank. Interesting here that there is a barrier at the end, which makes sense, but this is often the pain point of distributed training with PyTorch + NCCL;

Measuring data loading: this is of minor interest, but I liked the idea of not iterating on data loader in the loop statement itself but manually calling next() to get the batches, that makes it easier to measure data loading, that they average at the end for each epoch;

Logging MFU (model FLOPS utilization): they also compute and log MFU, which is quite helpful;

Delete predictions before backward: titan also deletes the model predictions before the backward() call to avoid memory peaks. This can be quite effective since you really don’t need this tensor anymore and you can delete it immediately before the backward pass;

Reduction of NCCL timeout: after the first training step, they reduce the NCCL timeout from the default 10 min to 100 sec. This is nice if you have well behaved replicas code and don’t need to do anything more complex, but 100 sec is a very short timeout that I would be careful using, it might be a good fit for your load but if your replicas drift a bit more, then you will need to keep adding barriers to avoid timeouts that can be incredibly difficult to debug and cause a lot of headaches;

Distributed checkpointing with mid-epoch checkpoint support: this is a very cool implementation, it uses distributed checkpointing from PyTorch. They create some wrappers (e.g. for optimizer) where they implement the Stateful protocol to support checkpointing. They also use the StatefulDataLoader from torchdata to do checkpointing of mid-epoch data loader state;

Misc: there are of course other interesting things, but it is cool to mention that they also implemented a no frills LLaMA model without relying on thousands of different libs (it seems it became fashionable nowadays to keep adding dependencies), so kudos for that to keep it simple.

21/08/202421/08/2024 by Christian S. Perone

Machine Learning, Programming

Memory-mapped CPU tensor between Torch, Numpy, Jax and TensorFlow

This is just a fun experiment to answer the question: how can I share a memory-mapped tensor from PyTorch to Numpy, Jax and TensorFlow in CPU without copy and making sure changes done in memory by torch are reflected on all these shared tensors ?

One approach is shown below:

import torch
import tensorflow as tf
import numpy as np
import jax.numpy as jnp
import jax.dlpack

# Create the tensor and persist
t = torch.randn(10, dtype=torch.float32)
t.numpy().tofile("tensor.pt")

# Memory-map the file with PyTorch
t_mapped = torch.from_file("tensor.pt", shared=True, size=10, dtype=torch.float32)

# Memory-map it with numpy, the same tensor
n_mapped = np.memmap("tensor.pt", dtype='float32', mode='r+', shape=(10))

# Convert it to Jax, will reuse the same buffer
j_mapped = jnp.asarray(n_mapped)

# Convert it to dlpack capsule and load in TensorFlow
dlcapsule = jax.dlpack.to_dlpack(j_mapped)
tf_mapped = tf.experimental.dlpack.from_dlpack(dlcapsule)

Now the fun part begins, I will change the tensor in PyTorch and we will check what happens in the Numpy, Jax and TensorFlow tensors:

>>> t_mapped.fill_(42.0) # Changing only PyTorch tensorA
tensor([42., 42., 42., 42., 42., 42., 42., 42., 42., 42.])

>>> n_mapped # Numpy Array
memmap([42., 42., 42., 42., 42., 42., 42., 42., 42., 42.], dtype=float32)

>>> j_mapped # Jax Array
Array([42., 42., 42., 42., 42., 42., 42., 42., 42., 42.], dtype=float32)

>>> tf_mapped # TensorFlow Tensor
<tf.Tensor: shape=(10,), dtype=float32, numpy=array([42., 42., 42., 42., 42., 42., 42., 42., 42., 42.], dtype=float32)>

As you can see from above, changes in the torch tensor reflected back into Numpy, Jax and TensorFlow, that’s the magic of memmap().

13/08/202413/08/2024 by Christian S. Perone

Machine Learning, Programming

VectorVFS: your filesystem as a vector database

PS: thanks for all the interest, here you are some discussions about VectorVFS as well:
Hacker News: discussion thread
Reddit: discussion thread

When I released EuclidesDB in 2018, which was the first modern vector database before milvus, pinecone, etc, I ended up still missing a piece of simple software for retrieval that can be local, easy to use and without requiring a daemon or any other sort of server and external indexes. After quite some time trying to figure it out what would be the best way to store embeddings in the filesystem I ended up in the design of VectorVFS.

timeline

The main goal of VectorVFS is to store the data embeddings (vectors) into the filesystem itself without requiring an external database. We don’t want to change the file contents as well and we also don’t want to create extra loose files in the filesystem. What we want is to store the embeddings on the files themselves without changing its data. How can we accomplish that ?

It turns out that all major Linux file systems (e.g. Ext4, Btrfs, ZFS, and XFS) support a feature that is called extended attributes (also known as xattr). This metadata is stored in the inode itself (ona reserved space at the end of each inode) and not in the data blocks (depending on the size). Some file systems might impose limits on the attributes, Ext4 for example requires them to be within a file system block (e.g. 4kb).

That is exactly what VectorVFS do, it embeds files (right now only images) using an encoder (Perception Encoder for the moment) and then it stores this embedding into the extended attributes of the file in the filesystem so we don’t need to create any other file for the metadata, the embedding will also be automatically linked directly to the file that was embedded and there is also no risks of this embedding being copied by mistake. It seems almost like a perfect solution for storing embeddings and retrieval that were there in many filesystems but it was never explored for that purpose before.

If you are interested, here is the documentation on how to install and use it, contributions are welcome !

29/04/202506/05/2025 by Christian S. Perone

Machine Learning, Math

The geometry of data: the missing metric tensor and the Stein score [Part II]

Credit: ESA/Webb, NASA & CSA, J. Rigby. / The James Webb Space Telescope captures gravitational lensing, a phenomenon that can be modeled using differential geometry.

Note: This is a continuation of the previous post: Thoughts on Riemannian metrics and its connection with diffusion/score matching [Part I], so if you haven’t read it yet, please consider reading as I won’t be re-introducing in depth the concepts (e.g., the two scores) that I described there already. This article became a bit long, so if you are familiar already with metric tensors and differential geometry you can just skip the first part.

I was planning to write a paper about this topic, but my spare time is not that great so I decided it would be much more fun and educative to write this article in form of a tutorial. If you liked it, please consider citing it:

Cite this article as: Christian S. Perone, "The geometry of data: the missing metric tensor and the Stein score [Part II]," in Terra Incognita, 12/11/2024, https://blog.christianperone.com/2024/11/the-geometry-of-data-part-ii/.

(more…)

12/11/202417/11/2024 by Christian S. Perone

Introduction

Diffusion Elites

Overview diagram

The big picture

Tags