Given the interesting recent article on “The Emergence of a Fovea while Learning to Attend“, I decide to make a review of the paper written by Luo, Wenjie et al. called “Understanding the Effective Receptive Field in Deep Convolutional Neural Networks” where they introduced the idea of the “Effective Receptive Field” (ERF) and the surprising relationship with the foveal vision that arises naturally on Convolutional Neural Networks.

The receptive field in Convolutional Neural Networks (CNN) is the region of the input space that affects a particular unit of the network. Note that this input region can be not only the input of the network but also output from other units in the network, therefore this receptive field can be calculated relative to the input that we consider and also relative the unit that we are taking into consideration as the “receiver” of this input region. Usually, when the receptive field term is mentioned, it is taking into consideration the final output unit of the network (i.e. a single unit on a binary classification task) in relation to the network input (i.e. input image of the network).

It is easy to see that on a CNN, the receptive field can be increased using different methods such as: stacking more layers (depth), subsampling (pooling, striding), filter dilation (dilated convolutions), etc. In theory, when you stack more layers you can increase your receptive field linearly, however, in practice, things aren’t simple as we thought, as shown by Luo, Wenjie et al. article. In the article, they introduce the concept of the “Effective Receptive Field”, or ERF; the intuition behind the concept is that not all pixels in the receptive field contribute equally to the output unit’s response. When doing the forward pass, we can see that the central receptive field pixels can propagate their information to the output using many different paths, as they are part of multiple output unit’s calculations.

In the figure below, we can see in left the input pixels, after that we have a feature map calculated from the input pixels using a 3×3 convolution filter and then finally the output after another 3×3 filtering. The numbers inside the pixels on the left image represent how many times this pixel was part of a convolution step (each sliding step of the filter). As we can see, some pixels like the central ones will have their information propagated through many different paths in the network, while the pixels on the borders are propagated along a single path.

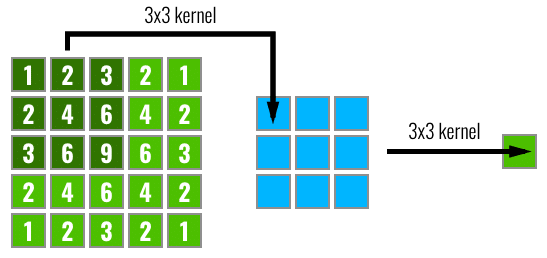
By looking at the image above, it isn’t that surprising that the effective receptive field impact on the final output computation will look more like a Gaussian distribution instead of a uniform distribution. What is actually more even interesting is that this receptive field is dynamic and changes during the training. The impact of this on the backpropagation is that the central pixels will have a larger gradient magnitude when compared to the border pixels.

In the article written by Luo, Wenjie et al., they devised a way to quantify the effect on each input pixel of the network by calculating the quantity that represents how much each pixel contributes to the output .

In the paper, they did experimentations to visualize the effective receptive field using multiple different architectures, activations, etc. I replicate here the ones that I found most interesting:

As we can see from the Figure 1 of the paper, where they compare the effect of the number of layers, initialization schemes, and different activations, the results are amazing. We can clearly see the Gaussian and also the sparsity added by the ReLU activations.

There are also some comparisons on Figure 3 of the paper, where CIFAR-10 and CamVid datasets were used to train the network.

As we can see, the size of the effective receptive field is very dynamic and it is increased by a large margin after the training, which implies, as stated by authors of the paper, that better initialization schemes can be employed to increase the receptive field in the beginning of the training. They actually developed a different initialization scheme and were able to get 30% training speed-up, however, these results weren’t consistent.

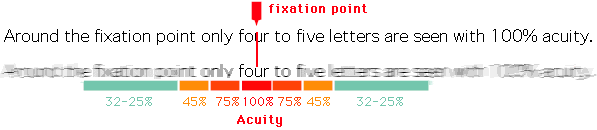
What is also very interesting, is that the effective receptive field has a very close relationship with the foveal vision of the human eye, which produces the sharp central vision, effect of the high-density region of cone cells (as shown in the image below) present in the eye fundus.

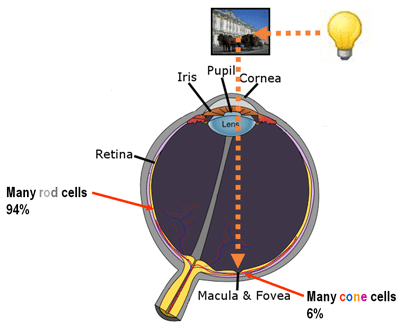
Our central sharp vision also decays rapidly like the effective receptive field that is very similar to a Gaussian. It is amazing that this effect is also naturally present on the CNN networks.

PS: Just for the sake of curiosity, some birds that do complex aerial movements such as the hummingbird, have two foveas instead of a single one, which means that they have a sharp accurate vision not only on the central region but also on the sides.

I hope you enjoyed the post !

– Christian S. Perone