by Christian S. Perone
Just sharing ~100 slides about PyTorch 2 internals focusing on recent innovations (Dynamo, Inductor, and ExecuTorch). I had a lot of fun preparing this and hope you’ll enjoy it. I’m planning to record it soon.
We are so used to Euclidean geometry that we often overlook the significance of curved geometries and the methods for measuring things that don’t reside on orthonormal bases. Just as understanding physics and the curvature of spacetime requires Riemannian geometry, I believe a profound comprehension of Machine Learning (ML) and data is also not possible without it. There is an increasing body of research that integrates differential geometry into ML. Unfortunately, the term “geometric deep learning” has predominantly become associated with graphs. However, modern geometry offers much more than just graph-related applications in ML.
I was reading the excellent article from Sander Dieleman about different perspectives on diffusion, so I thought it would be cool to try to contribute a bit with a new perspective.
We have been training language models (LMs) for years, but finding valuable resources about the data pipelines commonly used to build the datasets for training these models is paradoxically challenging. It may be because we often take it for granted that these datasets exist (or at least existed? As replicating them is becoming increasingly difficult). However, one must consider the numerous decisions involved in creating such pipelines, as it can significantly impact the final model’s quality, as seen recently in the struggle of models aiming to replicate LLaMA (LLaMA: Open and Efficient Foundation Language Models). It might be tempting to think that now, with large models that can scale well, data is becoming more critical than modeling, since model architectures are not radically changing much. However, data has always been critical.
This article provides a short introduction to the pipeline used to create the data to train LLaMA, but it allows for many variations and I will add details about other similar pipelines when relevant, such as RefinedWeb (The RefinedWeb Dataset for Falcon LLM: Outperforming Curated Corpora with Web Data, and Web Data Only) and The Pile (The Pile: An 800GB Dataset of Diverse Text for Language Modeling). This article is mainly based on the pipeline described in CCNet (CCNet: Extracting High Quality Monolingual Datasets from Web Crawl Data) and LLaMA’s paper, both from Meta. CCNet was developed focusing on the data source that is often the largest one, but also the most challenging in terms of quality: Common Crawl.
The entire pipeline of CCNet (plus some minor modifications made by LLaMA’s paper) can be seen below. It has the following stages: data source, deduplication, language, filtering, and the “is-reference” filtering which was added in LLaMA. I will go through each one of them in the sections below.
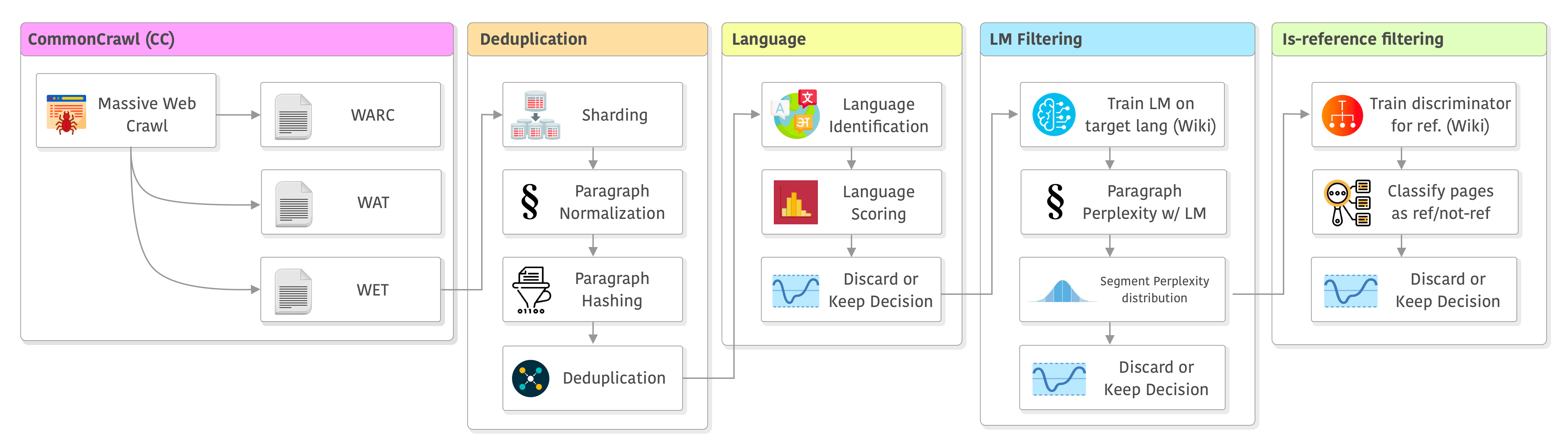
Let’s dive into it !
I just released Feste, a free and open-source framework with a permissive license that allows scalable composition of NLP tasks using a graph execution model that is optimized and executed by specialized schedulers. The main idea behind Feste is that it builds a graph of execution instead of executing tasks immediately, this graph allows Feste to optimize and parallelize it. One main example of optimization is when we have multiple calls to the same backend (e.g. same API), Feste automatically fuses these calls into a single one and therefore it batches the call to reduce latency and improve backend inference leverage of GPU vectorization. Feste also executes tasks that can be done in parallel in different processes, so the user doesn’t have to care about parallelization, especially when there are multiple frameworks using different concurrency strategies.
Project page: https://feste.readthedocs.io/en/latest/design.html
Github: https://github.com/perone/feste