Machine Learning :: Text feature extraction (tf-idf) – Part II
Read the first part of this tutorial: Text feature extraction (tf-idf) – Part I.
This post is a continuation of the first part where we started to learn the theory and practice about text feature extraction and vector space model representation. I really recommend you to read the first part of the post series in order to follow this second post.
Since a lot of people liked the first part of this tutorial, this second part is a little longer than the first.
Introduction
In the first post, we learned how to use the term-frequency to represent textual information in the vector space. However, the main problem with the term-frequency approach is that it scales up frequent terms and scales down rare terms which are empirically more informative than the high frequency terms. The basic intuition is that a term that occurs frequently in many documents is not a good discriminator, and really makes sense (at least in many experimental tests); the important question here is: why would you, in a classification problem for instance, emphasize a term which is almost present in the entire corpus of your documents ?
The tf-idf weight comes to solve this problem. What tf-idf gives is how important is a word to a document in a collection, and that’s why tf-idf incorporates local and global parameters, because it takes in consideration not only the isolated term but also the term within the document collection. What tf-idf then does to solve that problem, is to scale down the frequent terms while scaling up the rare terms; a term that occurs 10 times more than another isn’t 10 times more important than it, that’s why tf-idf uses the logarithmic scale to do that.
But let’s go back to our definition of the which is actually the term count of the term
in the document
. The use of this simple term frequency could lead us to problems like keyword spamming, which is when we have a repeated term in a document with the purpose of improving its ranking on an IR (Information Retrieval) system or even create a bias towards long documents, making them look more important than they are just because of the high frequency of the term in the document.
To overcome this problem, the term frequency of a document on a vector space is usually also normalized. Let’s see how we normalize this vector.
Vector normalization
Suppose we are going to normalize the term-frequency vector that we have calculated in the first part of this tutorial. The document
from the first part of this tutorial had this textual representation:
d4: We can see the shining sun, the bright sun.
And the vector space representation using the non-normalized term-frequency of that document was:
To normalize the vector, is the same as calculating the Unit Vector of the vector, and they are denoted using the “hat” notation: . The definition of the unit vector
of a vector
is:
Where the is the unit vector, or the normalized vector, the
is the vector going to be normalized and the
is the norm (magnitude, length) of the vector
in the
space (don’t worry, I’m going to explain it all).
The unit vector is actually nothing more than a normalized version of the vector, is a vector which the length is 1.
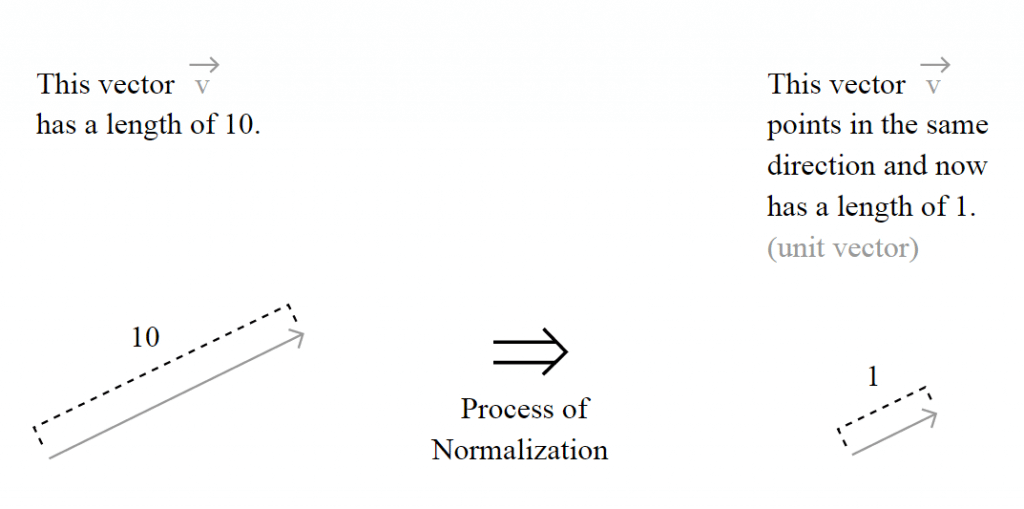
But the important question here is how the length of the vector is calculated and to understand this, you must understand the motivation of the spaces, also called Lebesgue spaces.
Lebesgue spaces
Usually, the length of a vector is calculated using the Euclidean norm – a norm is a function that assigns a strictly positive length or size to all vectors in a vector space -, which is defined by:
But this isn’t the only way to define length, and that’s why you see (sometimes) a number together with the norm notation, like in
. That’s because it could be generalized as:
and simplified as:
So when you read about a L2-norm, you’re reading about the Euclidean norm, a norm with , the most common norm used to measure the length of a vector, typically called “magnitude”; actually, when you have an unqualified length measure (without the
number), you have the L2-norm (Euclidean norm).
When you read about a L1-norm, you’re reading about the norm with , defined as:
Which is nothing more than a simple sum of the components of the vector, also known as Taxicab distance, also called Manhattan distance.
Taxicab geometry versus Euclidean distance: In taxicab geometry all three pictured lines have the same length (12) for the same route. In Euclidean geometry, the green line has length , and is the unique shortest path.
Source: Wikipedia :: Taxicab Geometry
Note that you can also use any norm to normalize the vector, but we’re going to use the most common norm, the L2-Norm, which is also the default in the 0.9 release of the scikits.learn. You can also find papers comparing the performance of the two approaches among other methods to normalize the document vector, actually you can use any other method, but you have to be concise, once you’ve used a norm, you have to use it for the whole process directly involving the norm (a unit vector that used a L1-norm isn’t going to have the length 1 if you’re going to take its L2-norm later).
Back to vector normalization
Now that you know what the vector normalization process is, we can try a concrete example, the process of using the L2-norm (we’ll use the right terms now) to normalize our vector in order to get its unit vector
. To do that, we’ll simple plug it into the definition of the unit vector to evaluate it:
And that is it ! Our normalized vector has now a L2-norm
.
Note that here we have normalized our term frequency document vector, but later we’re going to do that after the calculation of the tf-idf.
The term frequency – inverse document frequency (tf-idf) weight
Now you have understood how the vector normalization works in theory and practice, let’s continue our tutorial. Suppose you have the following documents in your collection (taken from the first part of tutorial):
Train Document Set: d1: The sky is blue. d2: The sun is bright. Test Document Set: d3: The sun in the sky is bright. d4: We can see the shining sun, the bright sun.
Your document space can be defined then as where
is the number of documents in your corpus, and in our case as
and
. The cardinality of our document space is defined by
and
, since we have only 2 two documents for training and testing, but they obviously don’t need to have the same cardinality.
Let’s see now, how idf (inverse document frequency) is then defined:
where is the number of documents where the term
appears, when the term-frequency function satisfies
, we’re only adding 1 into the formula to avoid zero-division.
The formula for the tf-idf is then:
and this formula has an important consequence: a high weight of the tf-idf calculation is reached when you have a high term frequency (tf) in the given document (local parameter) and a low document frequency of the term in the whole collection (global parameter).
Now let’s calculate the idf for each feature present in the feature matrix with the term frequency we have calculated in the first tutorial:
Since we have 4 features, we have to calculate ,
,
,
:
These idf weights can be represented by a vector as:
Now that we have our matrix with the term frequency () and the vector representing the idf for each feature of our matrix (
), we can calculate our tf-idf weights. What we have to do is a simple multiplication of each column of the matrix
with the respective
vector dimension. To do that, we can create a square diagonal matrix called
with both the vertical and horizontal dimensions equal to the vector
dimension:
and then multiply it to the term frequency matrix, so the final result can be defined then as:
Please note that the matrix multiplication isn’t commutative, the result of will be different than the result of the
, and this is why the
is on the right side of the multiplication, to accomplish the desired effect of multiplying each idf value to its corresponding feature:
Let’s see now a concrete example of this multiplication:
And finally, we can apply our L2 normalization process to the matrix. Please note that this normalization is “row-wise” because we’re going to handle each row of the matrix as a separated vector to be normalized, and not the matrix as a whole:
And that is our pretty normalized tf-idf weight of our testing document set, which is actually a collection of unit vectors. If you take the L2-norm of each row of the matrix, you’ll see that they all have a L2-norm of 1.
Python practice
Environment Used: Python v.2.7.2, Numpy 1.6.1, Scipy v.0.9.0, Sklearn (Scikits.learn) v.0.9.
Now the section you were waiting for ! In this section I’ll use Python to show each step of the tf-idf calculation using the Scikit.learn feature extraction module.
The first step is to create our training and testing document set and computing the term frequency matrix:
from sklearn.feature_extraction.text import CountVectorizer
train_set = ("The sky is blue.", "The sun is bright.")
test_set = ("The sun in the sky is bright.",
"We can see the shining sun, the bright sun.")
count_vectorizer = CountVectorizer()
count_vectorizer.fit_transform(train_set)
print "Vocabulary:", count_vectorizer.vocabulary
# Vocabulary: {'blue': 0, 'sun': 1, 'bright': 2, 'sky': 3}
freq_term_matrix = count_vectorizer.transform(test_set)
print freq_term_matrix.todense()
#[[0 1 1 1]
#[0 2 1 0]]
Now that we have the frequency term matrix (called freq_term_matrix), we can instantiate the TfidfTransformer, which is going to be responsible to calculate the tf-idf weights for our term frequency matrix:
from sklearn.feature_extraction.text import TfidfTransformer tfidf = TfidfTransformer(norm="l2") tfidf.fit(freq_term_matrix) print "IDF:", tfidf.idf_ # IDF: [ 0.69314718 -0.40546511 -0.40546511 0. ]
Note that I’ve specified the norm as L2, this is optional (actually the default is L2-norm), but I’ve added the parameter to make it explicit to you that it it’s going to use the L2-norm. Also note that you can see the calculated idf weight by accessing the internal attribute called idf_. Now that fit() method has calculated the idf for the matrix, let’s transform the freq_term_matrix to the tf-idf weight matrix:
tf_idf_matrix = tfidf.transform(freq_term_matrix) print tf_idf_matrix.todense() # [[ 0. -0.70710678 -0.70710678 0. ] # [ 0. -0.89442719 -0.4472136 0. ]]
And that is it, the tf_idf_matrix is actually our previous matrix. You can accomplish the same effect by using the Vectorizer class of the Scikit.learn which is a vectorizer that automatically combines the CountVectorizer and the TfidfTransformer to you. See this example to know how to use it for the text classification process.
I really hope you liked the post, I tried to make it simple as possible even for people without the required mathematical background of linear algebra, etc. In the next Machine Learning post I’m expecting to show how you can use the tf-idf to calculate the cosine similarity.
If you liked it, feel free to comment and make suggestions, corrections, etc.
References
Understanding Inverse Document Frequency: on theoretical arguments for IDF
The classic Vector Space Model
Sklearn text feature extraction code
Updates
13 Mar 2015 – Formating, fixed images issues.
03 Oct 2011 – Added the info about the environment used for Python examples

Wow!
Perfect intro in tf-idf, thank you very much! Very interesting, I’ve wanted to study this field for a long time and you posts it is a real gift. It would be very interesting to read more about use-cases of the technique. And may be you’ll be interested, please, to shed some light on other methods of text corpus representation, if they exists?
(sorry for bad English, I’m working to improve it, but there is still a lot of job to do)
Excellent work Christian! I am looking forward to reading your next posts on document classification, clustering and topics extraction with Naive Bayes, Stochastic Gradient Descent, Minibatch-k-Means and Non Negative Matrix factorization 🙂
Also, the documentation of scikit-learn is really poor on the text feature extraction part (I am the main culprit…). Don’t hesitate to join the mailing list if you want to give a hand and improve upon the current situation.
Great thanks Olivier. I really want to help sklearn, I just have to get some more time to do that, you guys have done a great work, I’m really impressed by the amount of algorithms already implemented in the lib, keep the good work !
I like this tutorial better for the level of new concepts i am learning here.
That said, which version of scikits-learn are you using?.
The latest as installed by easy_install seems to have a different module hierarchy (i.e doesn’t find feature_extraction in sklearn). If you could mention the version you used, i will just try out with those examples.
Hello Anand, I’m glad you liked it. I’ve added the information about the environment used just before the section “Python practice”, I’m using the scikits.learn 0.9 (released a few weeks ago).
Where’s part 3? I’ve got to submit an assignment on Vector Space Modelling in 4 days. Any hope of putting it up over the weekend?
I’ve no date to publish it since I haven’t got any time to write it =(
Thanks again for this complete and explicit tutorial and I am waiting for the coming section.
Thanks Christian! a very nice work on vector space with sklearn. I just have one question, suppose I have computed the ‘tf_idf_matrix’, and I would like to compute the pair-wise cosine similarity (between each rows). I was having problem with the sparse matrix format, can you please give an example on that? Also my matrix is pretty big, say 25k by 60k. Thanks a lot!
Great post… I understand what tf-idf and how to implement it with a concrete example. But I caught 2 things that I’m not sure about:
1- You called the 2 dimensional matrix M_train, but it has the tf values of the D3 and D4 documents, so you should’ve called that matrix M_test instead of M_train. Because D3 and D4 are our test documents.
2- When you calculate the idf value for the t2 (which is ‘sun’) it should be log(2/4). Because number of the documents is 2. D3 has the word ‘sun’ 1 time, D4 has it 2 times. Which makes it 3 but we also add 1 to that value to get rid of divided by 0 problem. And this makes it 4… Am I right or am I missing something?
Thank you.
You are correct: these are excellent blog articles, but the author REALLY has a duty/responsibility to go back and correct errors, like this (and others, e.g. Part 1; …): missing training underscores; setting the stop_words parameter; also on my computer, the vocabulary indexing is different.
As much as we appreciate the effort (kudos to the author!), it is also a significant disservice to those who struggle past those (uncorrected) errors in the original material.
re: my ‘you are correct comment’ (above), I should have added:
“… noting also Frédérique Passot’s comment (below) regarding the denominator:
‘… what we are using is really the number of documents in which a term occurs, regardless of the number of times the term occurs in any given document. In this case, then, the denominator in the idf value for t2 (‘sun’) is indeed 2+1 (2 documents have the term ‘sun’, +1 to avoid a potential zero division error).’ “
Khalid,
This is a response to a very old question. However, I still want to respond to communicate what I understand from the article.
Your question 2: “When you calculate the idf value for the t2 (which is ‘sun’) it should be log(2/4)”
My understanding: The denominator in log term should be (number of documents in which the term appears + 1) and not frequency of the term. The number of documents the term “Sun” appears is 2 (1 time in D3 and 2 times in D4 — totally it appears 3 times in two documents. 3 is frequency and 2 is number of documents). Hence the denominator is 2 + 1 = 3.
thanks… excellent post…
excellent post!
I have some question. From the last tf-idf weight matrix, how can we get the importance of term respectively(e.g. which is the most important term?). How can we use this matrix to classify documents
Thank You So Much. You explained it in such a simple way. It was really useful. Once again thanks a lot.
I have same doubt as Jack(last comment). From the last tf-idf weight matrix, how can we get the importance of term respectively(e.g. which is the most important term?). How can we use this matrix to classify documents.
I have a question..
After the tf-idf operation, we get a numpy array with values. Suppose we need to get the highest 50 values from the array. How can we do that?
high value of f(idf) denotes that the particular vector(or Document) has high local strength and low global strength, in which case you can assume that the terms in it has high significance locally and cant be ignored. Comparing against funtion(tf) where only the term repeats high number of times are the ones given more importance,which most of the times is not a proper modelling technique.
Hey ,
Thanx fr d code..was very helpful indeed !
1.For document clustering,after calculating inverted term frequency, shud i use any associativity coefficient like Jaccards coefficient and then apply the clustering algo like k-means or shud i apply d k-means directly to the document vectors after calculating inverted term frequency ?
2. How do u rate inverted term frequency for calcuating document vectors for document clustering ?
Thanks a ton fr the forth coming reply! 😀
@Khalid: what you’re pointing out in 1- got me confused too for a minute (M_train vs M_test). I think you are mistaken on your second point, though, because what we are using is really the number of documents in which a term occurs, regardless of the number of times the term occurs in any given document. In this case, then, the denominator in the idf value for t2 (“sun”) is indeed 2+1 (2 documents have the term “sun”, +1 to avoid a potential zero division error).
I’d love to read the third installment of this series too! I’d be particularly interested in learning more about feature selection. Is there an idiomatic way to get a sorted list of the terms with the highest tf.idf scores? How would you identify those terms overall? How would you get the terms which are the most responsible for a high or low cosine similarity (row by row)?
Thank you for the _great_ posts!
Should idf(t2) be log 2/4 ?
Excellent article and a great introduction to td-idf normalization.
You have a very clear and structured way of explaining these difficult concepts.
Thanks!
Thanks for the feedback Matthys, I’m glad you liked the tutorial series.
very good & infomative tutorial…. please upload more tutorials related to documents clustering process.
Excellent article ! Thank you Christian. You did a great job.
Can you provide any reference for doing cosine similarity using tfidf so we have the matrix of tf-idf how can we use that to calculate cosine. Thanks for fantastic article.
Thanks so much for this and for explaining the whole tf-idf thing thoroughly.
Thanks for the feedback, I’m glad you liked the tutorial series.
Please correct me if i’m worng
the formula after starting with “frequency we have calculated in the first tutorial:” should Mtest not Mtrain. also after starting ‘These idf weights can be represented by a vector as:” should be idf_test not idf_train.
Btw great series, can you give an simple approach for how to implement classification?
Excellent it really helped me get through the concept of VSM and tf-idf. Thanks Christian
Very good post. Congrats!!
Showing your results, I have a question:
I read in the wikipedia:
The tf-idf value increases proportionally to the number of times a word appears in the document, but is offset by the frequency of the word in the corpus, which helps to control for the fact that some words are generally more common than others.
When I read it, I understand that if a word apperars in all documents is less important that a word that only appears in one document:
However, in the results, the word “sun” or “bright” are most important than “sky”.
I’m not sure of understand it completly.
Awesome! Explains TF-IDF very well. Waiting eagerly for your next post.
awesome work with a clear cut explanation . Even a layman can easily understand the subject..
Great thanks for the feedback Rahul !
Hello,
The explanation is awesome. I haven’t seen a better one yet. I have trouble reproducing the results. It might be because of some update of sklearn.
Would it be possible for you to update the code?
It seem that the formula for computing the tf-idf vector has changed a little bit. Is a typo or another formula. Below is the link to the source code.
https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/feature_extraction/text.py#L954
Many thanks
Terrific! I was familiar with tf-idf before but I found your scikits examples helpful as I’m trying to learn that package.
I’m glad you liked Susan, thanks for the feedback !
Thank you for writing such a detailed post. I learn allot.
Excellent post! Stumbled on this by chance looking for more information on CountVectorizer, but I’m glad I read through both of your posts (part 1 and part 2).
Bookmarking your blog now 🙂
Great thanks for the feedback Eugene, I’m really glad you liked the tutorial series.
Does not seem to fit_transform() as you describe..
Any idea why ?
>>> ts
(‘The sky is blue’, ‘The sun is bright’)
>>> v7 = CountVectorizer()
>>> v7.fit_transform(ts)
<2×2 sparse matrix of type '’
with 4 stored elements in COOrdinate format>
>>> print v7.vocabulary_
{u’is’: 0, u’the’: 1}
Actually, there are two small errors in the first Python sample.
1. CountVectorizer should be instantiated like so:
count_vectorizer = CountVectorizer(stop_words='english')This will make sure the ‘is’, ‘the’ etc are removed.
2. To print the vocabulary, you have to add an underscore at the end.
print "Vocabulary:", count_vectorizer.vocabulary_Excellent tutorial, just small things. hoep it helps others.
Thanks ash. although the article was rather self explanatory, your comment made the entire difference.
I loved your article.
I’m using scikit learn v .14. Is there any reason my results for running the exact same code would result in different results?
Thanks for taking time to write this article. Found it very useful.
Its useful…..thank you explaining the TD_IDF very elaborately..
Thanks for the great explanation.
I have a question about calculation of the idf(t#).
In the first case, you wrote idf(t1) = log(2/1), because we don’t have such term in our collection, thus, we add 1 to the denominator. Now, in case t2, you wrote log(2/3), why the denominator is equal to 3 and not to 4 (=1+2+1)? In case t3, you write: log(2/3), thus the denominator is equal 3 (=1+1+1). I see here kind of inconsistency. Could you, please, explain, how did calculate the denominator value.
Thanks.
Hello Mike, thanks for the feedback. You’re right, I just haven’t fixed it yet due to lack of time to review it and recalculate the values.
You got it wrong, in the denominator you don’t put the sum of the term in each document, you just sum all the documents that have at least one aparition of the term.
yes, I had the same question…
This is good post
it is good if you can provide way to know how use ft-idf in classification of document. I see that example (python code) but if there is algorithm that is best because no all people can understand this language.
Thanks
Great post, really helped me understand the tf-idf concept!
Nice Post
Nice. An explanation helps put things into perspective. Is tf-idf a good way to do clustering (e.g. use Jaccard analysis or variance against the average set from a known corpus)?
Keep writing:)
Hi Christian,
It makes me very excited and lucky to have read this article. The clarity of your understanding reflects in the clarity of the document. It makes me regain my confidence in the field of machine learning.
Thanks a ton for the beautiful explanation.
Would like to read more from you.
Thanks,
Neethu
Great thanks for the kind wors Neethu ! I’m very glad you liked the tutorial series.
thank you very very much,very wonderful and useful.
Thanks for the feedback Esra’a.
Thank you for the good wrap up. You mention a number of papers which compare L1 and L2 norm, I plan to study that a bit more in depth. You still know their names?
how can i calculate tf idf for my own text file which is located some where in my pc?
Brilliant article.
By far the easiest and most sound explanation of tf-tdf I’ve read. I really liked how you explained the mathematics behind it.
superb article for newbies
Excellent material. Excellent!!!
Hi, great post! I’m using the TfidVectorizer module in scikit learn to produce the tf-idf matrix with norm=l2. I’ve been examining the output of the TfidfVectorizer after fit_transform of the corpora which I called tfidf_matrix. I’ve summed the rows but they do not sum to 1. The code is vect = TfidfVectorizer(use_idf=True, sublunar_tf=True, norm=”l2). tfidf_matrix = vect.fit_transform(data). When I run tfidf_matrix.sum(axis=1) the vectors are larger than 1. Perhaps I’m looking at the wrong matrix or I misunderstand how normalisation works. I hope someone can clarify this point! Thanks
Can I ask when you calculated the IDF, for example, log(2/1), did you use log to base 10 (e) or some other value? I’m getting different calculations!
Great tutorial, just started a new job in ML and this explains things very clearly as it should be.
Execellent post….!!! Thanks alot for this article.
But I need more information, As you show the practical with python, Can you provide it with JAVA language..
I’m a little bit confused why tf-idf gives negative numbers in this case? How do we interpret them? Correct me if I am wrong, but when the vector has a positive value, it means that the magnitude of that component determines how important that word is in that document. If the it is negative, I don’t know how to interpret it. If I were to take the dot product of a vector with all positive components and one with negative components, it would mean that some components may contribute negatively to the dot product even though on of the vectors has very high importance for a particular word.
Hi,
thank you so much for this detailed explanation on this topic, really great. Anyway, could you give me a hint what could be the source of my error that I am keep on seeing:
freq_term_matrix = count_vectorizer.transform(test_set)
AttributeError: ‘matrix’ object has no attribute ‘transform’
Am I using a wrong version of sklearn?
Awesome simple and effective explaination.Please post more topics with such awesome explainations.Looking forward for upcoming articles.
Thanks 🙂
Thank you Chris, you are the only one on the web who was clear about the diagonal matrix.
Great tutorial for Tf-Idf. Excellent work . Please add for cosine similarity also:)
I understood the tf-idf calculation process. But what does that matrix mean and how can we use the tfidf matrix to calculate the similarity confuse me. can you explain that how can we use the tfidf matrix .thanks
thx for your explict&detailed explaination.
thanks, nice post, I’m trying it out
Thank you so much for such an amazing detailed explanation!
best explanation.. Very helpful. Can you please tell me how to plot vectors in text classification in svm.. I am working on tweets classification. I am confused please help me.
I learned so many things. Thanks Christian. Looking forward for your next tutorial.
Hi, I’m sorry if i have mistaken but i could not understand how is ||Vd4||2 = 1.
the value of d4 = (0.0 ,0.89,0.44,0.0) so the normalization will be = sqrt( square(.89)+square(.44))=sqrt(.193) = .44
so what did i missed ? please help me to understand .
Hi, it is a great blog!
If I need to do bi-gram cases, how can I use sklearn to finish it?
it is very great. i love your teach. very very good
I am not getting same result, when i am executing the same script.
print (“IDF:”, tfidf.idf_) : IDF: [ 2.09861229 1. 1.40546511 1. ]
My python version is: 3.5
Scikit Learn version is: o.18.1
what does i need to change? what might be the possible error?
thanks,
It can be many things, since you’re using a different Python interpreter version and also a different Scikit-Learn version, you should expect differences in the results since they may have changed default parameters, algorithms, rounding, etc.
I am also getting: IDF: [2.09861229 1. 1.40546511 1. ]
Perfect introduction!
No hocus pocus. Clear and simple, as technology should be.
Very helpful
Thank you very much.
Keep posting!
Obrigado
Why is |D| = 2, in the idf equation. Shouldn’t it be 4 since |D| denotes the number of documents considered, and we have 2 from test, 2 from train.
This post is interesting. I like this post…
clear cut and to the point explanations….great
hey , hii Christian
your post is really helpful to me to understand tfd-idf from the basics. I’m working on a project of classification where I’m using vector space model which results in determining the categories where my test document should be present. its a part of machine learning . it would be great if you suggest me something related to that. I’m stuck at this point.
thank you
See this example to know how to use it for the text classification process. “This” link does not work any more. Can you please provide a relevant link for the example.
Thanks
such a great explanation! thankyou!
wow, awesome post.Much thanks again. Will read on
Say, you got a nice post.Really thank you! Fantastic.
Wow, great article post.Much thanks again. Awesome.
There is certainly a great deal to learn about this subject. I really like all the points you made.
1vbXlh You have brought up a very wonderful details , appreciate it for the post.
I know this site provides quality based articles or
reviews and additional data, is there any other web page which presents these kinds of
information in quality?
In the first example. idf(t1), the log (2/1) = 0.3010 by the calculator. Why they obtained 0.69.. Please What is wrong?
Hi, I really liked your explanation clear and straight to the point.
I have just one question.
In the part when you calculate the IDF for the term t2 (that i suppose to be the term ‘sun’) you put at the denominator a 3 and I’m wondering why it is not a 4, because I have ‘sun ‘1 time in the doc-3 and 2 time in the doc-4 as shown in the M train matrix above, so if i add them together is 3 and then in my denominator i have +1 so it’s suppose to be 4.