Python

News, Python, Science

An analysis of Benford’s law applied to Twitter

Benford’s law is one of those very weird things that we can’t explain, and when we discover more and more phenomena that obey the law, we became astonished. Two people (Simon Newcomb – 1881 and Frank Benford – 1938) noted the law in the same way, while flipping pages of a logarithmic table book; they noticed that the pages at the beginning of the book were dirtier than the pages at the end.

Currently, there are no a priori criteria that say to us when a dataset will or will not obey the Benford’s Law. And it is because of this, that I’ve done an analysis on the Twitter Public Timeline.

The Twitter API to get Public Timeline is simply useless for this analysis because in the API Docs, they say that the Public Timeline is cached for 60 seconds ! 60 seconds is an eternity, and there is a request rating of 150 request/hour. So, it doesn’t help, buuuuuut, there is an alpha testing API with pretty and very useful streams of data from the Public Timeline; there are many methods in the Twitter Streaming API, and the most interesting one is the “Firehose”, which returns ALL the public statuses, but this method is only available for intere$ting people, and I’m not one of them. Buuuut, we have “Spritzer”, which returns a portion of all public statuses, since it’s only what we have available in the moment, it MUST be useful, and it’s a pretty stream of data =)

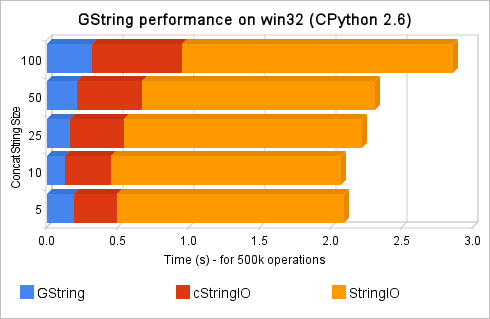
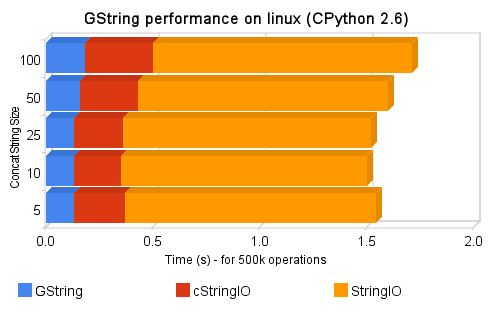
So, I’ve got the Spritzer real-time stream of data and processed each new status which arrived with a regex to find all the numbers in the status; if the status was “I have 5 dogs and 3 cats”, the numbers collected should be “[5, 3]”. All those accumulated numbers were then checked against the Benford’s Law. I’ve used Matplotlib to plot the two curves (the Benford’s Law and the Twitter statuses digits distribution) to empirically observe the correlation between them. You can note in the upper right corner of the video, the Pearson’s correlation between the two distributions too.

Here is the video (I’ve seen only after creating of the video, but the color of  the curves are the inverse as seen in the legend):

The video represents the 15 minutes (3.160 captured statuses) of the Twitter Public Timeline. At the end of the video, you can see a Pearson’s correlation of 0.95. It seems that we have found another Benford’s son =)

The little tool to handle the Twitter Spritzer stream of data and plot the correlation graph in real-time was entirely written in Python, I’ll do a clean-up and post it here soon I got time. The tool has generated 1823 png images that were merged using ffmpeg.

I hope you enjoyed =)

Cite this article as: Christian S. Perone, "An analysis of Benford’s law applied to Twitter," in Terra Incognita, 11/08/2009, https://blog.christianperone.com/2009/08/an-analysis-of-benfords-law-applied-to-twitter/.

UPDATE 11/08: the user “poobare” has cited an interesting paper about Benford’s Law on Reddit, here is the link.

More posts about Benford’s Law

Prime Numbers and the Benford’s Law

Delicious.com, checking user numbers against Benford’s Law

Benford’s Law meets Python and Apple Stock Prices

by Christian S. Perone
Python

Announce: python-gstringc 1.0

Last week I’ve done the ctype wrapper of Glib GString, but the performance issues when compared with cStringIO or StringIO was very poor, due to overhead of the ctypes calls. So I’ve written a new C extension for Python, the source-code (for linux) and install packages (for win32) are available at the project site. Here is some performance comparisons:

gstring

gstring_linux

Those tests were done to test string concatenation (append) of the three modules. You can find more about the tests and performance in the project site.

I hope you enjoy =)

by Christian S. Perone
Python

GLib GString wrapper for Python

I’ve done a little wrapper of GLib/GString functionality using Python ctypes. GString of GLib is an amazing and very stable work done by GLib team, the core used by GTK+ and many other libraries. The wrapper I’ve done works in Windows and Linux, but the performance results seems more interesting for Windows, however, the GString functionality is very interesting for any platform. The project is hosted here in Google project hosting.

Here is some examples of the wrapper:

>>> from GString import GString
>>> obj1 = GString("test")
>>> obj1

>>> print obj1
test
>>> obj1+obj1

>>> obj1+=obj1
>>> obj1

>>> obj1.truncate(5)

>>> obj1.insert(2, "xx")

>>> obj1.assign("test")

>>> obj1.erase(2,2)

>>> obj1.assign("12345")
>>> for i in xrange(len(obj1)):
...    print obj1[i]
...
1
2
3
4
5

I hope you enjoyed the wrapper, you can find performance comparisons in the project home site.

by Christian S. Perone
java, Python

Jinja2 in a Java JSP

This is a simple trick possible using Jython; to call jinja2 template engine under JSP we instantiate the PythonInterpreter class of Jython, set some parameters in the interpreter and then call jinja2 to render a template and write to the Java “out” object.

To install Jython, just download the last stable version Jython 2.5 and then install it as “Standalone” version; the installer will create a simple jython.jar file under the installation directory, copy this package to your Java web project under the \WEB-INF\lib or where you put your web application libraries.

Later, copy the jinja2 module to the \build\classes.

Create a simple template under the WebContent\templates\template.html with contents below:

This is just a Jinja2 template test !

Parameter "p" = {{ request.getParameter("p") }}

Getting session attribute: {{ session.getAttribute("session_attribute") }}

Iterating over Java array:

    
{% for user in users %}
	
  • {{ user }}
    • 
{% endfor %}

And now create a file called index.jsp in the root of the WebContent, with the contents:

<%@ page language="java" contentType="text/html; charset=ISO-8859-1"
    pageEncoding="ISO-8859-1"%>
<%@page import="org.python.util.PythonInterpreter" %>




Jinja2 Template under JSP


<%
	PythonInterpreter py = new PythonInterpreter();

	String[] users = {"User Number One", "User Number Two"};
	session.setAttribute("session_attribute", "Testing Session");
	
	py.set("out",     out);
	py.set("request", request);
	py.set("session", session);
	py.set("users",   users);
	py.set("context_path", application.getRealPath("/") + "templates");
		
	py.exec("from jinja2 import Environment, FileSystemLoader");
	py.exec("env = Environment(loader=FileSystemLoader(context_path))");
	py.exec("template = env.get_template('template.html')");
	py.exec("out.write(template.render(locals()))");
%>

The structure will be like this:

structure

And the output will be something like this:

out

by Christian S. Perone
genetic programming, News, Pyevolve, Python, Time Waste

Approximating Pi number using Genetic Programming

pi

As many (or very few in the real life haha) people know, today is the Pi Approximation Day ! So it’s time to make a contribution to celebrate this funny day =)

My contribution is to use Python and Pyevolve to approximate Pi number using Genetic Programming approach. I’ve created the functions gp_add(+), gp_sub(-), gp_div(/), gp_mul(*) and gp_sqrt (square root) to use as non-terminals of the GP. The fitness function is very simple too, it simple returns the absolute difference between the Python math.pi and the evaluated individual. I’ve used also a population size of 1k individuals with max tree depth of 8 and the random ephemeral constants as random integers. The best approximation I’ve got while running the GP for about 8 minutes (40 generations) was 3.1416185511, best for 3 digits, you can improve it and let it run for more time to get better approximations.

Here is the formulae I’ve got with the GP (click to enlarge):

tree_pi

And here is the output of the script:

Best (0): 3.1577998365
        Error: 0.0162071829
Best (10): 3.1417973679
        Error: 0.0002047143
Best (20): 3.1417973679
        Error: 0.0002047143
Best (30): 3.1417973679
        Error: 0.0002047143
Best (40): 3.1416185511
        Error: 0.0000258975

- GenomeBase
        Score:                   0.000026
        Fitness:                 15751.020831

        Params:          {'max_depth': 8, 'method': 'ramped'}

        Slot [Evaluator] (Count: 1)
        Slot [Initializator] (Count: 1)
                Name: GTreeGPInitializator - Weight: 0.50
                Doc: This initializator accepts the follow parameters:

   *max_depth*
      The max depth of the tree

   *method*
      The method, accepts "grow" or "full"

   .. versionadded:: 0.6
      The *GTreeGPInitializator* function.

        Slot [Mutator] (Count: 1)
                Name: GTreeGPMutatorSubtree - Weight: 0.50
                Doc:  The mutator of GTreeGP, Subtree Mutator

   .. versionadded:: 0.6
      The *GTreeGPMutatorSubtree* function

        Slot [Crossover] (Count: 1)
                Name: GTreeGPCrossoverSinglePoint - Weight: 0.50

- GTree
        Height:                 8
        Nodes:                  21

GTreeNodeBase [Childs=1] - [gp_sqrt]
  GTreeNodeBase [Childs=2] - [gp_div]
    GTreeNodeBase [Childs=2] - [gp_add]
      GTreeNodeBase [Childs=0] - [26]
      GTreeNodeBase [Childs=2] - [gp_div]
        GTreeNodeBase [Childs=2] - [gp_mul]
          GTreeNodeBase [Childs=2] - [gp_add]
            GTreeNodeBase [Childs=2] - [gp_sub]
              GTreeNodeBase [Childs=0] - [34]
              GTreeNodeBase [Childs=2] - [gp_sub]
                GTreeNodeBase [Childs=0] - [44]
                GTreeNodeBase [Childs=0] - [1]
            GTreeNodeBase [Childs=2] - [gp_mul]
              GTreeNodeBase [Childs=0] - [49]
              GTreeNodeBase [Childs=0] - [43]
          GTreeNodeBase [Childs=1] - [gp_sqrt]
            GTreeNodeBase [Childs=0] - [18]
        GTreeNodeBase [Childs=0] - [16]
    GTreeNodeBase [Childs=2] - [gp_add]
      GTreeNodeBase [Childs=0] - [24]
      GTreeNodeBase [Childs=0] - [35]

- GTreeGP
        Expression: gp_sqrt(gp_div(gp_add(26,
gp_div(gp_mul(gp_add(gp_sub(34,
gp_sub(44, 1)), gp_mul(49, 43)), gp_sqrt(18)),
16)), gp_add(24, 35)))

And finally, here is the source code:

from __future__ import division
from pyevolve import *
import math

def gp_add(a, b): return a+b
def gp_sub(a, b): return a-b
def gp_div(a, b): return 1 if b==0 else a/b
def gp_mul(a, b): return a*b
def gp_sqrt(a):   return math.sqrt(abs(a))

def eval_func(chromosome):
   code_comp = chromosome.getCompiledCode()
   ret = eval(code_comp)
   return abs(math.pi - ret)

def step_callback(engine):
   gen = engine.getCurrentGeneration()
   if gen % 10 == 0:
      best = engine.bestIndividual()
      best_pi = eval(best.getCompiledCode())
      print "Best (%d): %.10f" % (gen, best_pi)
      print "\tError: %.10f" % (abs(math.pi - best_pi))

   return False

def main_run():
   genome = GTree.GTreeGP()

   genome.setParams(max_depth=8, method="ramped")
   genome.evaluator += eval_func

   ga = GSimpleGA.GSimpleGA(genome)
   ga.setParams(gp_terminals       = ['ephemeral:random.randint(1, 50)'],
                gp_function_prefix = "gp")

   ga.setMinimax(Consts.minimaxType["minimize"])
   ga.setGenerations(50000)
   ga.setCrossoverRate(1.0)
   ga.setMutationRate(0.09)
   ga.setPopulationSize(1000)
   ga.stepCallback.set(step_callback)

   ga.evolve()
   best = ga.bestIndividual()
   best.writeDotImage("tree_pi.png")

   print best

if __name__ == "__main__":
   main_run()

If you are interested why today is the Pi Approximation day, see some resources:

Little Cartoon

Some Background History

Some Pi Approximations

by Christian S. Perone
genetic programming, Pyevolve, Python

Genetic Programming and Flex layouts

To show how Genetic Programming of Pyevolve can be flexible, I’ve done a simple example using Adobe Flex and Pyevolve, the example is just to show how to evolve some kind of Flex layouts, I’ve not implemented the fitness function, this example will just create a random Flex layout using MXML. So, here is the Pyevolve code of the example:

import random
from pyevolve import *

def gp_hbox(x, y):
   return "%s %s" % (x,y)

def gp_vbox(x, y):
   return "%s %s" % (x,y)

def gp_panel(x, y):
   return "%s %s" % (x,y)

def eval_func(chromosome):
   code_comp = chromosome.getCompiledCode()

   for a in xrange(0, 5):
      for b in xrange(0, 5):
         evaluated     = eval(code_comp)
   return random.randint(1,100)

def main_run():
   genome = GTree.GTreeGP()
   genome.setParams(max_depth=5, method="ramped")
   genome.evaluator += eval_func

   ga = GSimpleGA.GSimpleGA(genome)

   button     = repr("<mx:Button label='Button'/>")
   label      = repr("<mx:Label text='Label'/>")
   text_input = repr("<mx:TextInput width='50'/>")

   ga.setParams(gp_terminals       = [button, label, text_input],
                gp_function_prefix = "gp")
   ga.setMinimax(Consts.minimaxType["minimize"])
   ga.evolve(freq_stats=5)
   print ga.bestIndividual()

if __name__ == "__main__":
   main_run()

As you can see, I’ve created the layout tags like HBox, VBox and Panel as functions of GP and the Button, Labe, TextInput as terminals of the GP, the result is very funny, it’s just a random layout, but you can use your imagination to create some nice and interesting fitness functions.

Here is the SWF generated from a random individual of the population:

I hope you enjoyed =)

by Christian S. Perone
genetic programming, Pyevolve, Python

Genetic Programming meets Python

I’m proud to announce that the new versions of Pyevolve will have Genetic Programming support; after some time fighting with these evil syntax trees, I think I have a very easy and flexible implementation of GP in Python. I was tired to see people giving up and trying to learn how to implement a simple GP using the hermetic libraries for C/C++ and Java (unfortunatelly I’m a Java web developer hehe).

The implementation is still under some tests and optimization, but it’s working nice, here is some details about it:

The implementation has been done in pure Python, so we still have many bonus from this, but unfortunatelly we lost some performance.

The GP core is very very flexible, because it compiles the GP Trees in Python bytecodes to speed the execution of the function. So, you can use even Python objects as terminals, or any possible Python expression. Any Python function can be used too, and you can use all power of Python to create those functions, which will be automatic detected by the framework using the name prefix =)

As you can see in the source-code, you don’t need to bind variables when calling the syntax tree of the individual, you simple use the “getCompiledCode” method which returns the Python compiled function ready to be executed.

Here is a source-code example:

from pyevolve import *
import math

error_accum = Util.ErrorAccumulator()

# This is the functions used by the GP core,
# Pyevolve will automatically detect them
# and the they number of arguments
def gp_add(a, b): return a+b
def gp_sub(a, b): return a-b
def gp_mul(a, b): return a*b
def gp_sqrt(a):   return math.sqrt(abs(a))

def eval_func(chromosome):
   global error_accum
   error_accum.reset()
   code_comp = chromosome.getCompiledCode()

   for a in xrange(0, 5):
      for b in xrange(0, 5):
         # The eval will execute a pre-compiled syntax tree
         # as a Python expression, and will automatically use
         # the "a" and "b" variables (the terminals defined)
         evaluated     = eval(code_comp)
         target        = math.sqrt((a*a)+(b*b))
         error_accum += (target, evaluated)
   return error_accum.getRMSE()

def main_run():
   genome = GTree.GTreeGP()
   genome.setParams(max_depth=5, method="ramped")
   genome.evaluator.set(eval_func)

   ga = GSimpleGA.GSimpleGA(genome)
   # This method will catch and use every function that
   # begins with "gp", but you can also add them manually.
   # The terminals are Python variables, you can use the
   # ephemeral random consts too, using ephemeral:random.randint(0,2)
   # for example.
   ga.setParams(gp_terminals       = ['a', 'b'],
                gp_function_prefix = "gp")
   # You can even use a function call as terminal, like "func()"
   # and Pyevolve will use the result of the call as terminal
   ga.setMinimax(Consts.minimaxType["minimize"])
   ga.setGenerations(1000)
   ga.setMutationRate(0.08)
   ga.setCrossoverRate(1.0)
   ga.setPopulationSize(2000)
   ga.evolve(freq_stats=5)

   print ga.bestIndividual()

if __name__ == "__main__":
   main_run()

I’m very happy and testing the possibilities of this GP implementation in Python.

And of course, everything in Pyevolve can be visualized any time you want (click to enlarge):

ramped_small

ramped_big

The visualization is very flexible too, if you use Python decorators to set how functions will be graphical represented, you can have many interesting visualization patterns. If I change the function “gp_add” to:

@GTree.gpdec(representation="+", color="red")
def gp_add(a, b): return a+b

We’ll got the follow visualization (click to enlarge):

full

I hope you enjoyed it, I’m currently fixing some bugs, implementing new features, docs and preparing the next release of Pyevolve, which will take some time yet =)

by Christian S. Perone