Update: Hacker News discussion here.
The TensorFlow Computation Graph

One of the most amazing components of the TensorFlow architecture is the computation graph that can be serialized using Protocol Buffers. This computation graph follows a well-defined format (click here for the proto files) and describes the computation that you specify (it can be a Deep Learning model like a CNN, a simple Logistic Regression or even any computation you want). For instance, here is an example of a very simple TensorFlow computation graph that we will use in this tutorial (using TensorFlow Python API):
import tensorflow as tf
with tf.Session() as sess:
input_placeholder = tf.placeholder(tf.int32, 1, name="input")
sub_op = tf.sub(input_placeholder, tf.constant(2, dtype=tf.int32))
add_op = tf.add(sub_op, tf.constant(5, dtype=tf.int32))
output = tf.add(add_op, tf.constant(100, dtype=tf.int32),
name="output")
tf.train.write_graph(sess.graph_def, ".", "graph.pb", True)
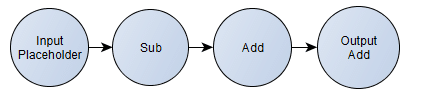
As you can see, this is a very simple computation graph. First, we define the placeholder that will hold the input tensor and after that we specify the computation that should happen using this input tensor as input data. Here we can also see that we’re defining two important nodes of this graph, one is called “input” (the aforementioned placeholder) and the other is called “output“, that will hold the result of the final computation. This graph is the same as the following formula for a scalar: , where I intentionally added redundant operations to see LLVM constant propagation later.
In the last line of the code, we’re persisting this computation graph (including the constant values) into a serialized protobuf file. The final True parameter is to output a textual representation instead of binary, so it will produce the following human-readable output protobuf file (I omitted a part of it for brevity):
node {
name: "input"
op: "Placeholder"
attr {
key: "dtype"
value {
type: DT_INT32
}
}
attr {
key: "shape"
value {
shape {
dim {
size: 1
}
}
}
}
}
node {
name: "Const"
op: "Const"
attr {
key: "dtype"
value {
type: DT_INT32
}
}
attr {
key: "value"
value {
tensor {
dtype: DT_INT32
tensor_shape {
}
int_val: 2
}
}
}
}
--- >(omitted for brevity) < ---
node {
name: "output"
op: "Add"
input: "Add"
input: "Const_2"
attr {
key: "T"
value {
type: DT_INT32
}
}
}
versions {
producer: 9
}
This is a very simple graph, and TensorFlow graphs are actually never that simple, because TensorFlow models can easily contain more than 300 nodes depending on the model you’re specifying, specially for Deep Learning models.
We’ll use the above graph to show how we can JIT native code for this simple graph using LLVM framework.
The LLVM Frontend, IR and Backend

The LLVM framework is a really nice, modular and complete ecosystem for building compilers and toolchains. A very nice description of the LLVM architecture that is important for us is shown in the picture below:
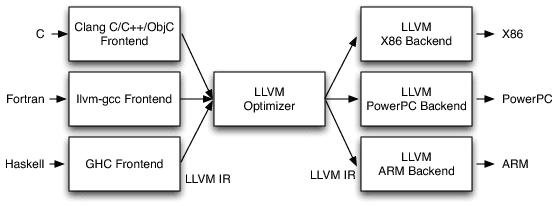
(The picture above is just a small part of the LLVM architecture, for a comprehensive description of it, please see the nice article from the AOSA book written by Chris Lattner)
Looking in the image above, we can see that LLVM provides a lot of core functionality, in the left side you see that many languages can write code for their respective language frontends, after that it doesn’t matter in which language you wrote your code, everything is transformed into a very powerful language called LLVM IR (LLVM Intermediate Representation) which is as you can imagine, a intermediate representation of the code just before the assembly code itself. In my opinion, the IR is the key component of what makes LLVM so amazing, because it doesn’t matter in which language you wrote your code (or even if it was a JIT’ed IR), everything ends in the same representation, and then here is where the magic happens, because the IR can take advantage of the LLVM optimizations (also known as transform and analysis passes).
After this IR generation, you can feed it into any LLVM backend to generate native code for any architecture supported by LLVM (such as x86, ARM, PPC, etc) and then you can finally execute your code with the native performance and also after LLVM optimization passes.
In order to JIT code using LLVM, all you need is to build the IR programmatically, create a execution engine to convert (during execution-time) the IR into native code, get a pointer for the function you have JIT’ed and then finally execute it. I’ll use here a Python binding for LLVM called llvmlite, which is very Pythonic and easy to use.
JIT’ing TensorFlow Graph using Python and LLVM

Let’s now use the LLVM and Python to JIT the TensorFlow computational graph. This is by no means a comprehensive implementation, it is very simplistic approach, a oversimplification that assumes some things: a integer closure type, just some TensorFlow operations and also a single scalar support instead of high rank tensors.
So, let’s start building our JIT code; first of all, let’s import the required packages, initialize some LLVM sub-systems and also define the LLVM respective type for the TensorFlow integer type:
from ctypes import CFUNCTYPE, c_int
import tensorflow as tf
from google.protobuf import text_format
from tensorflow.core.framework import graph_pb2
from tensorflow.core.framework import types_pb2
from tensorflow.python.framework import ops
import llvmlite.ir as ll
import llvmlite.binding as llvm
llvm.initialize()
llvm.initialize_native_target()
llvm.initialize_native_asmprinter()
TYPE_TF_LLVM = {
types_pb2.DT_INT32: ll.IntType(32),
}
After that, let’s define a class to open the TensorFlow exported graph and also declare a method to get a node of the graph by name:
class TFGraph(object):
def __init__(self, filename="graph.pb", binary=False):
self.graph_def = graph_pb2.GraphDef()
with open("graph.pb", "rb") as f:
if binary:
self.graph_def.ParseFromString(f.read())
else:
text_format.Merge(f.read(), self.graph_def)
def get_node(self, name):
for node in self.graph_def.node:
if node.name == name:
return node
And let’s start by defining our main function that will be the starting point of the code:
def run_main():
graph = TFGraph("graph.pb", False)
input_node = graph.get_node("input")
output_node = graph.get_node("output")
input_type = TYPE_TF_LLVM[input_node.attr["dtype"].type]
output_type = TYPE_TF_LLVM[output_node.attr["T"].type]
module = ll.Module()
func_type = ll.FunctionType(output_type, [input_type])
func = ll.Function(module, func_type, name='tensorflow_graph')
func.args[0].name = 'input'
bb_entry = func.append_basic_block('entry')
ir_builder = ll.IRBuilder(bb_entry)
As you can see in the code above, we open the serialized protobuf graph and then get the input and output nodes of this graph. After that we also map the type of the both graph nodes (input/output) to the LLVM type (from TensorFlow integer to LLVM integer). We start then by defining a LLVM Module, which is the top level container for all IR objects. One module in LLVM can contain many different functions, here we will create just one function that will represent the graph, this function will receive as input argument the input data of the same type of the input node and then it will return a value with the same type of the output node.
After that we start by creating the entry block of the function and using this block we instantiate our IR Builder, which is a object that will provide us the building blocks for JIT’ing operations of TensorFlow graph.
Let’s now define the function that will do the real work of converting TensorFlow nodes into LLVM IR:
def build_graph(ir_builder, graph, node):
if node.op == "Add":
left_op_node = graph.get_node(node.input[0])
right_op_node = graph.get_node(node.input[1])
left_op = build_graph(ir_builder, graph, left_op_node)
right_op = build_graph(ir_builder, graph, right_op_node)
return ir_builder.add(left_op, right_op)
if node.op == "Sub":
left_op_node = graph.get_node(node.input[0])
right_op_node = graph.get_node(node.input[1])
left_op = build_graph(ir_builder, graph, left_op_node)
right_op = build_graph(ir_builder, graph, right_op_node)
return ir_builder.sub(left_op, right_op)
if node.op == "Placeholder":
function_args = ir_builder.function.args
for arg in function_args:
if arg.name == node.name:
return arg
raise RuntimeError("Input [{}] not found !".format(node.name))
if node.op == "Const":
llvm_const_type = TYPE_TF_LLVM[node.attr["dtype"].type]
const_value = node.attr["value"].tensor.int_val[0]
llvm_const_value = llvm_const_type(const_value)
return llvm_const_value
In this function, we receive by parameters the IR Builder, the graph class that we created earlier and the output node. This function will then recursively build the LLVM IR by means of the IR Builder. Here you can see that I only implemented the Add/Sub/Placeholder and Const operations from the TensorFlow graph, just to be able to support the graph that we defined earlier.
After that, we just need to define a function that will take a LLVM Module and then create a execution engine that will execute the LLVM optimization over the LLVM IR before doing the hard-work of converting the IR into native x86 code:
def create_engine(module):
features = llvm.get_host_cpu_features().flatten()
llvm_module = llvm.parse_assembly(str(module))
target = llvm.Target.from_default_triple()
target_machine = target.create_target_machine(opt=3, features=features)
engine = llvm.create_mcjit_compiler(llvm_module, target_machine)
engine.finalize_object()
print target_machine.emit_assembly(llvm_module)
return engine
In the code above, you can see that we first get the CPU features (SSE, etc) into a list, after that we parse the LLVM IR from the module and then we create a engine using maximum optimization level (opt=3, roughly equivalent to the GCC -O3 parameter), we’re also printing the assembly code (in my case, the x86 assembly built by LLVM).
And here we just finish our run_main() function:
ret = build_graph(ir_builder, graph, output_node)
ir_builder.ret(ret)
with open("output.ir", "w") as f:
f.write(str(module))
engine = create_engine(module)
func_ptr = engine.get_function_address("tensorflow_graph")
cfunc = CFUNCTYPE(c_int, c_int)(func_ptr)
ret = cfunc(10)
print "Execution output: {}".format(ret)
As you can see in the code above, we just call the build_graph() method and then use the IR Builder to add the “ret” LLVM IR instruction (ret = return) to return the output of the IR function we just created based on the TensorFlow graph. We’re also here writing the IR output to a external file, I’ll use this LLVM IR file later to create native assembly for other different architectures such as ARM architecture. And finally, just get the native code function address, create a Python wrapper for this function and then call it with the argument “10”, which will be input data and then output the resulting output value.
And that is it, of course that this is just a oversimplification, but now we understand the advantages of having a JIT for our TensorFlow models.
The output LLVM IR, the advantage of optimizations and multiple architectures (ARM, PPC, x86, etc)
For instance, lets create the LLVM IR (using the code I shown above) of the following TensorFlow graph:
import tensorflow as tf
with tf.Session() as sess:
input_placeholder = tf.placeholder(tf.int32, 1, name="input")
sub_op = tf.sub(input_placeholder, tf.constant(2, dtype=tf.int32))
add_op = tf.add(sub_op, tf.constant(5, dtype=tf.int32))
output = tf.add(add_op, tf.constant(100, dtype=tf.int32),
name="output")
tf.train.write_graph(sess.graph_def, ".", "graph.pb", True)
The LLVM IR generated is this one below:
; ModuleID = ""
target triple = "unknown-unknown-unknown"
target datalayout = ""
define i32 @"tensorflow_graph"(i32 %"input")
{
entry:
%".3" = sub i32 %"input", 2
%".4" = add i32 %".3", 5
%".5" = add i32 %".4", 100
ret i32 %".5"
}
As you can see, the LLVM IR looks a lot like an assembly code, but this is not the final assembly code, this is just a non-optimized IR yet. Just before generating the x86 assembly code, LLVM runs a lot of optimization passes over the LLVM IR, and it will do things such as dead code elimination, constant propagation, etc. And here is the final native x86 assembly code that LLVM generates for the above LLVM IR of the TensorFlow graph:
.text
.file "<string>"
.globl tensorflow_graph
.align 16, 0x90
.type tensorflow_graph,@function
tensorflow_graph:
.cfi_startproc
leal 103(%rdi), %eax
retq
.Lfunc_end0:
.size tensorflow_graph, .Lfunc_end0-tensorflow_graph
.cfi_endproc
.section ".note.GNU-stack","",@progbits
As you can see, the optimized code removed a lot of redundant operations, and ended up just doing a add operation of 103, which is the correct simplification of the computation that we defined in the graph. For large graphs, you can see that these optimizations can be really powerful, because we are reusing the compiler optimizations that were developed for years in our Machine Learning model computation.
You can also use a LLVM tool called “llc”, that can take an LLVM IR file and the generate assembly for any other platform you want, for instance, the command-line below will generate native code for ARM architecture:
llc -O3 out.ll -march=arm -o sample.s
The output sample.s file is the one below:
.text
.syntax unified
.eabi_attribute 67, "2.09" @ Tag_conformance
.eabi_attribute 6, 1 @ Tag_CPU_arch
.eabi_attribute 8, 1 @ Tag_ARM_ISA_use
.eabi_attribute 17, 1 @ Tag_ABI_PCS_GOT_use
.eabi_attribute 20, 1 @ Tag_ABI_FP_denormal
.eabi_attribute 21, 1 @ Tag_ABI_FP_exceptions
.eabi_attribute 23, 3 @ Tag_ABI_FP_number_model
.eabi_attribute 34, 1 @ Tag_CPU_unaligned_access
.eabi_attribute 24, 1 @ Tag_ABI_align_needed
.eabi_attribute 25, 1 @ Tag_ABI_align_preserved
.eabi_attribute 38, 1 @ Tag_ABI_FP_16bit_format
.eabi_attribute 14, 0 @ Tag_ABI_PCS_R9_use
.file "out.ll"
.globl tensorflow_graph
.align 2
.type tensorflow_graph,%function
tensorflow_graph: @ @tensorflow_graph
.fnstart
@ BB#0: @ %entry
add r0, r0, #103
mov pc, lr
.Lfunc_end0:
.size tensorflow_graph, .Lfunc_end0-tensorflow_graph
.fnend
.section ".note.GNU-stack","",%progbits
As you can see above, the ARM assembly code is also just a “add” assembly instruction followed by a return instruction.
This is really nice because we can take natural advantage of the LLVM framework. For instance, today ARM just announced the ARMv8-A with Scalable Vector Extensions (SVE) that will support 2048-bit vectors, and they are already working on patches for LLVM. In future, a really nice addition to LLVM would be the development of LLVM Passes for analysis and transformation that would take into consideration the nature of Machine Learning models.
And that’s it, I hope you liked the post ! Is really awesome what you can do with a few lines of Python, LLVM and TensorFlow.
Update 22 Aug 2016: Josh Klontz just pointed his cool project called Likely on Hacker News discussion.
Update 22 Aug 2016: TensorFlow team is actually working on a JIT (I don’t know if they are using LLVM, but it seems the most reasonable way to go in my opinion). In their paper, there is also a very important statement regarding Future Work that I cite here:
“We also have a number of concrete directions to improve the performance of TensorFlow. One such direction is our initial work on a just-in-time compiler that can take a subgraph of a TensorFlow execution, perhaps with some runtime profiling information about the typical sizes and shapes of tensors, and can generate an optimized routine for this subgraph. This compiler will understand the semantics of perform a number of optimizations such as loop fusion, blocking and tiling for locality, specialization for particular shapes and sizes, etc.” – TensorFlow White Paper
Full code
from ctypes import CFUNCTYPE, c_int
import tensorflow as tf
from google.protobuf import text_format
from tensorflow.core.framework import graph_pb2
from tensorflow.core.framework import types_pb2
from tensorflow.python.framework import ops
import llvmlite.ir as ll
import llvmlite.binding as llvm
llvm.initialize()
llvm.initialize_native_target()
llvm.initialize_native_asmprinter()
TYPE_TF_LLVM = {
types_pb2.DT_INT32: ll.IntType(32),
}
class TFGraph(object):
def __init__(self, filename="graph.pb", binary=False):
self.graph_def = graph_pb2.GraphDef()
with open("graph.pb", "rb") as f:
if binary:
self.graph_def.ParseFromString(f.read())
else:
text_format.Merge(f.read(), self.graph_def)
def get_node(self, name):
for node in self.graph_def.node:
if node.name == name:
return node
def build_graph(ir_builder, graph, node):
if node.op == "Add":
left_op_node = graph.get_node(node.input[0])
right_op_node = graph.get_node(node.input[1])
left_op = build_graph(ir_builder, graph, left_op_node)
right_op = build_graph(ir_builder, graph, right_op_node)
return ir_builder.add(left_op, right_op)
if node.op == "Sub":
left_op_node = graph.get_node(node.input[0])
right_op_node = graph.get_node(node.input[1])
left_op = build_graph(ir_builder, graph, left_op_node)
right_op = build_graph(ir_builder, graph, right_op_node)
return ir_builder.sub(left_op, right_op)
if node.op == "Placeholder":
function_args = ir_builder.function.args
for arg in function_args:
if arg.name == node.name:
return arg
raise RuntimeError("Input [{}] not found !".format(node.name))
if node.op == "Const":
llvm_const_type = TYPE_TF_LLVM[node.attr["dtype"].type]
const_value = node.attr["value"].tensor.int_val[0]
llvm_const_value = llvm_const_type(const_value)
return llvm_const_value
def create_engine(module):
features = llvm.get_host_cpu_features().flatten()
llvm_module = llvm.parse_assembly(str(module))
target = llvm.Target.from_default_triple()
target_machine = target.create_target_machine(opt=3, features=features)
engine = llvm.create_mcjit_compiler(llvm_module, target_machine)
engine.finalize_object()
print target_machine.emit_assembly(llvm_module)
return engine
def run_main():
graph = TFGraph("graph.pb", False)
input_node = graph.get_node("input")
output_node = graph.get_node("output")
input_type = TYPE_TF_LLVM[input_node.attr["dtype"].type]
output_type = TYPE_TF_LLVM[output_node.attr["T"].type]
module = ll.Module()
func_type = ll.FunctionType(output_type, [input_type])
func = ll.Function(module, func_type, name='tensorflow_graph')
func.args[0].name = 'input'
bb_entry = func.append_basic_block('entry')
ir_builder = ll.IRBuilder(bb_entry)
ret = build_graph(ir_builder, graph, output_node)
ir_builder.ret(ret)
with open("output.ir", "w") as f:
f.write(str(module))
engine = create_engine(module)
func_ptr = engine.get_function_address("tensorflow_graph")
cfunc = CFUNCTYPE(c_int, c_int)(func_ptr)
ret = cfunc(10)
print "Execution output: {}".format(ret)
if __name__ == "__main__":
run_main()
