Approximating Pi number using Genetic Programming
As many (or very few in the real life haha) people know, today is the Pi Approximation Day ! So it’s time to make a contribution to celebrate this funny day =)
My contribution is to use Python and Pyevolve to approximate Pi number using Genetic Programming approach. I’ve created the functions gp_add(+), gp_sub(-), gp_div(/), gp_mul(*) and gp_sqrt (square root) to use as non-terminals of the GP. The fitness function is very simple too, it simple returns the absolute difference between the Python math.pi and the evaluated individual. I’ve used also a population size of 1k individuals with max tree depth of 8 and the random ephemeral constants as random integers. The best approximation I’ve got while running the GP for about 8 minutes (40 generations) was 3.1416185511, best for 3 digits, you can improve it and let it run for more time to get better approximations.
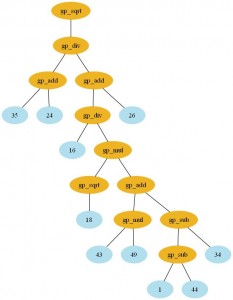
Here is the formulae I’ve got with the GP (click to enlarge):
And here is the output of the script:
Best (0): 3.1577998365
Error: 0.0162071829
Best (10): 3.1417973679
Error: 0.0002047143
Best (20): 3.1417973679
Error: 0.0002047143
Best (30): 3.1417973679
Error: 0.0002047143
Best (40): 3.1416185511
Error: 0.0000258975
- GenomeBase
Score: 0.000026
Fitness: 15751.020831
Params: {'max_depth': 8, 'method': 'ramped'}
Slot [Evaluator] (Count: 1)
Slot [Initializator] (Count: 1)
Name: GTreeGPInitializator - Weight: 0.50
Doc: This initializator accepts the follow parameters:
*max_depth*
The max depth of the tree
*method*
The method, accepts "grow" or "full"
.. versionadded:: 0.6
The *GTreeGPInitializator* function.
Slot [Mutator] (Count: 1)
Name: GTreeGPMutatorSubtree - Weight: 0.50
Doc: The mutator of GTreeGP, Subtree Mutator
.. versionadded:: 0.6
The *GTreeGPMutatorSubtree* function
Slot [Crossover] (Count: 1)
Name: GTreeGPCrossoverSinglePoint - Weight: 0.50
- GTree
Height: 8
Nodes: 21
GTreeNodeBase [Childs=1] - [gp_sqrt]
GTreeNodeBase [Childs=2] - [gp_div]
GTreeNodeBase [Childs=2] - [gp_add]
GTreeNodeBase [Childs=0] - [26]
GTreeNodeBase [Childs=2] - [gp_div]
GTreeNodeBase [Childs=2] - [gp_mul]
GTreeNodeBase [Childs=2] - [gp_add]
GTreeNodeBase [Childs=2] - [gp_sub]
GTreeNodeBase [Childs=0] - [34]
GTreeNodeBase [Childs=2] - [gp_sub]
GTreeNodeBase [Childs=0] - [44]
GTreeNodeBase [Childs=0] - [1]
GTreeNodeBase [Childs=2] - [gp_mul]
GTreeNodeBase [Childs=0] - [49]
GTreeNodeBase [Childs=0] - [43]
GTreeNodeBase [Childs=1] - [gp_sqrt]
GTreeNodeBase [Childs=0] - [18]
GTreeNodeBase [Childs=0] - [16]
GTreeNodeBase [Childs=2] - [gp_add]
GTreeNodeBase [Childs=0] - [24]
GTreeNodeBase [Childs=0] - [35]
- GTreeGP
Expression: gp_sqrt(gp_div(gp_add(26,
gp_div(gp_mul(gp_add(gp_sub(34,
gp_sub(44, 1)), gp_mul(49, 43)), gp_sqrt(18)),
16)), gp_add(24, 35)))
And finally, here is the source code:
from __future__ import division
from pyevolve import *
import math
def gp_add(a, b): return a+b
def gp_sub(a, b): return a-b
def gp_div(a, b): return 1 if b==0 else a/b
def gp_mul(a, b): return a*b
def gp_sqrt(a): return math.sqrt(abs(a))
def eval_func(chromosome):
code_comp = chromosome.getCompiledCode()
ret = eval(code_comp)
return abs(math.pi - ret)
def step_callback(engine):
gen = engine.getCurrentGeneration()
if gen % 10 == 0:
best = engine.bestIndividual()
best_pi = eval(best.getCompiledCode())
print "Best (%d): %.10f" % (gen, best_pi)
print "\tError: %.10f" % (abs(math.pi - best_pi))
return False
def main_run():
genome = GTree.GTreeGP()
genome.setParams(max_depth=8, method="ramped")
genome.evaluator += eval_func
ga = GSimpleGA.GSimpleGA(genome)
ga.setParams(gp_terminals = ['ephemeral:random.randint(1, 50)'],
gp_function_prefix = "gp")
ga.setMinimax(Consts.minimaxType["minimize"])
ga.setGenerations(50000)
ga.setCrossoverRate(1.0)
ga.setMutationRate(0.09)
ga.setPopulationSize(1000)
ga.stepCallback.set(step_callback)
ga.evolve()
best = ga.bestIndividual()
best.writeDotImage("tree_pi.png")
print best
if __name__ == "__main__":
main_run()
If you are interested why today is the Pi Approximation day, see some resources:

This does the job :).
def pi(n):
second, x = False, 1.0
for i in range(3, n * 2 + 1, 2):
if second:
x += 1.0 / i
else:
x -= 1.0 /i
second = not second
return 4 * x
>>> pi(1e7)
3.1415925535897915
and
def test_pi():
from time import time
t = time()
pi(1e7)
return time() - t
>>> test_pi()
3.87999…
See the Eq. 26 in http://mathworld.wolfram.com/PiApproximations.html
Christian, I would really like to try this. But I am having some problems with PyEvolve. I have python 2.6 on linux. I used easy-install to install the egg (also ver. 2.6). However, I keep getting this error:
webbge@webbge-laptop:~/Desktop$ python pi_evolver.py
Traceback (most recent call last):
File “pi_evolver.py”, line 50, in
main_run()
File “pi_evolver.py”, line 27, in main_run
genome = GTree.GTreeGP()
NameError: global name ‘GTree’ is not defined
Any ideas would be greatly appreciated. Would love to play with pyevolve.
Hello, you must checkout the development release from the sourceforge subversion repository, the GP features are not available yet, this features will be part of the 0.6 release.
Thank you. Works great, no problems. Now I can evolve. Seems like a fun project. Good luck.
And it is =) thank you !
Sou aluno do curso de mestrado em Eng. Mec. da UNESP. Sou iniciante na área de programação evolucionária. Minha dissertação tem como título ” Escalonamento da produção Job-Shop com Algoritmos Genéticos”. Gostaria de saber se posso contar com seus conselhos. Grato desde já.
Opa Filipe, claro que pode contar sim, qualquer coisa que precisar é só falar, te adicionei lá no twitter. Abraço !
Sir,
Could you please give me an idea regarding how to do multi population genetic algorithm program.Can you please mail the sample program for multi population GA?
Regards ,
Anupama