A small intro on the rationale
So I’m working on a Symbolic Regression Machine written in C/C++ called Shine, which is intended to be a JIT for Genetic Programming libraries (like Pyevolve for instance). The main rationale behind Shine is that we have today a lot of research on speeding Genetic Programming using GPUs (the GPU fever !) or any other special hardware, etc, however we don’t have many papers talking about optimizing GP using the state of art compilers optimizations like we have on clang, gcc, etc.
The “hot spot” or the component that consumes a lot of CPU resources today on Genetic Programming is the evaluation of each individual in order to calculate the fitness of the program tree. This evaluation is often executed on each set of parameters of the “training” set. Suppose you want to make a symbolic regression of a single expression like the Pythagoras Theorem and you have a linear space of parameters from 1.0 to 1000.0 with a step of 0.1 you have 10.000 evaluations for each individual (program tree) of your population !
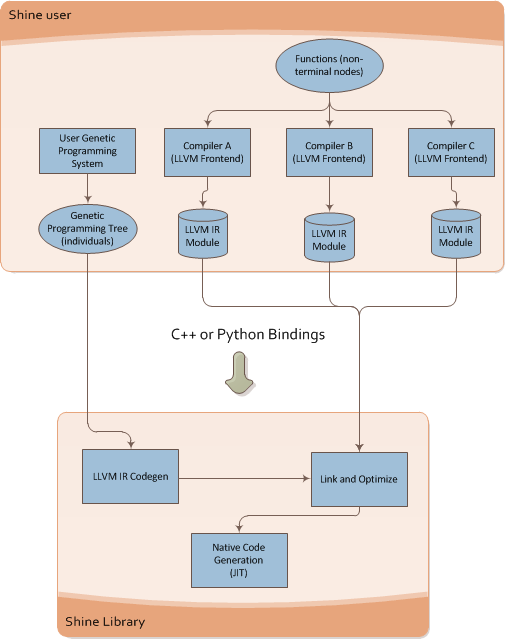
What Shine does is described on the image below:
It takes the individual of the Genetic Programming engine and then converts it to LLVM Intermediate Representation (LLVM assembly language), after that it runs the transformation passes of the LLVM (here is where the true power of modern compilers enter on the GP context) and then the LLVM JIT converts the optimized LLVM IR into native code for the specified target (X86, PowerPC, etc).
You can see below the Shine architecture:
This architecture brings a lot of flexibility for Genetic Programming, you can for instance write functions that could be used later on your individuals on any language supported by the LLVM, what matters to Shine is the LLVM IR, you can use any language that LLVM supports and then use the IR generated by LLVM, you can mix code from C, C++, Ada, Fortran, D, etc and use your functions as non-terminal nodes of your Genetic Programming trees.
Shine is still on its earlier development, it looks a simple idea but I still have a lot of problems to solve, things like how to JIT the evaluation process itself instead of doing calls from Python using ctypes bindings of the JITed trees.
Doing Genetic Programming on the Python AST itself
During the development of Shine, an idea happened to me, that I could use a restricted Python Abstract Syntax Tree (AST) as the representation of individuals on a Genetic Programming engine, the main advantage of this is the flexibility and the possibility to reuse a lot of things. Of course that a shared library written in C/C++ would be useful for a lot of Genetic Programming engines that doesn’t uses Python, but since my spare time to work on this is becoming more and more rare I started to rethink the approach and use Python and the LLVM bindings for LLVM (LLVMPY) and I just discovered that is pretty easy to JIT a restricted set of the Python AST to native code using LLVM, and this is what this post is going to show.
JIT’ing a restricted Python AST
The most amazing part of LLVM is obviously the amount of transformation passes, the JIT and of course the ability to use the entire framework through a simple API (ok, not so simple sometimes). To simplify this example, I’m going to use an arbitrary restricted AST set of the Python AST that supports only subtraction (-), addition (+), multiplication (*) and division (/).
To understand the Python AST, you can use the Python parser that converts source into AST:
>>> import ast
>>> astp = ast.parse("2*7")
>>> ast.dump(astp)
'Module(body=[Expr(value=BinOp(left=Num(n=2), op=Mult(), right=Num(n=7)))])'
What the parse created was an Abstract Syntax Tree containing the BinOp (Binary Operation) with the left operator as the number 2, the right operator as the number 7 and the operation itself as Multiplication(Mult), very easy to understand. What we are going to do to create the LLVM IR is to create a visitor that is going to visit each node of the tree. To do that, we can subclass the Python NodeVisitor class from the ast module. What the NodeVisitor does is to visit each node of the tree and then call the method ‘visit_OPERATOR’ if it exists, when the NodeVisitor is going to visit the node for the BinOp for example, it will call the method ‘visit_BinOp’ passing as parameter the BinOp node itself.
The structure of the class for for the JIT visitor will look like the code below:
# Import the ast and the llvm Python bindings
import ast
from llvm import *
from llvm.core import *
from llvm.ee import *
import llvm.passes as lp
class AstJit(ast.NodeVisitor):
def __init__(self):
pass
What we need to do now is to create an initialization method to keep the last state of the JIT visitor, this is needed because we are going to JIT the content of the Python AST into a function and the last instruction of the function needs to return what was the result of the last instruction visited by the JIT. We also need to receive a LLVM Module object in which our function will be created as well the closure type, for the sake of simplicity I’m not type any object, I’m just assuming that all numbers from the expression are integers, so the closure type will be the LLVM integer type.
def __init__(self, module, parameters):
self.last_state = None
self.module = module
# Parameters that will be created on the IR function
self.parameters = parameters
self.closure_type = Type.int()
# An attribute to hold a link to the created function
# so we can use it to JIT later
self.func_obj = None
self._create_builder()
def _create_builder(self):
# How many parameters of integer type
params = [self.closure_type] * len(self.parameters)
# The prototype of the function, returning a integer
# and receiving the integer parameters
ty_func = Type.function(self.closure_type, params)
# Add the function to the module with the name 'func_ast_jit'
self.func_obj = self.module.add_function(ty_func, 'func_ast_jit')
# Create an argument in the function for each parameter specified
for index, pname in enumerate(self.parameters):
self.func_obj.args[index].name = pname
# Create a basic block and the builder
bb = self.func_obj.append_basic_block("entry")
self.builder = Builder.new(bb)
Now what we need to implement on our visitor is the ‘visit_OPERATOR’ methods for the BinOp and for the Numand Name operators. We will also implement the method to create the return instruction that will return the last state.
# A 'Name' is a node produced in the AST when you
# access a variable, like '2+x+y', 'x' and 'y' are
# the two names created on the AST for the expression.
def visit_Name(self, node):
# This variable is what function argument ?
index = self.parameters.index(node.id)
self.last_state = self.func_obj.args[index]
return self.last_state
# Here we create a LLVM IR integer constant using the
# Num node, on the expression '2+3' you'll have two
# Num nodes, the Num(n=2) and the Num(n=3).
def visit_Num(self, node):
self.last_state = Constant.int(self.closure_type, node.n)
return self.last_state
# The visitor for the binary operation
def visit_BinOp(self, node):
# Get the operation, left and right arguments
lhs = self.visit(node.left)
rhs = self.visit(node.right)
op = node.op
# Convert each operation (Sub, Add, Mult, Div) to their
# LLVM IR integer instruction equivalent
if isinstance(op, ast.Sub):
op = self.builder.sub(lhs, rhs, 'sub_t')
elif isinstance(op, ast.Add):
op = self.builder.add(lhs, rhs, 'add_t')
elif isinstance(op, ast.Mult):
op = self.builder.mul(lhs, rhs, 'mul_t')
elif isinstance(op, ast.Div):
op = self.builder.sdiv(lhs, rhs, 'sdiv_t')
self.last_state = op
return self.last_state
# Build the return (ret) statement with the last state
def build_return(self):
self.builder.ret(self.last_state)
And that is it, our visitor is ready to convert a Python AST to a LLVM IR assembly language, to run it we’ll first create a LLVM module and an expression:
module = Module.new('ast_jit_module')
# Note that I'm using two variables 'a' and 'b'
expr = "(2+3*b+33*(10/2)+1+3/3+a)/2"
node = ast.parse(expr)
print ast.dump(node)
Will output:
Module(body=[Expr(value=BinOp(left=BinOp(left=BinOp(left=BinOp( left=BinOp(left=BinOp(left=Num(n=2), op=Add(), right=BinOp( left=Num(n=3), op=Mult(), right=Name(id='b', ctx=Load()))), op=Add(), right=BinOp(left=Num(n=33), op=Mult(), right=Num(n=2))), op=Add(), right=Num(n=1)), op=Add(), right=Num(n=3)), op=Add(), right=Name(id='a', ctx=Load())), op=Div(), right=Num(n=2)))])
Now we can finally run our visitor on that generated AST the check the LLVM IR output:
visitor = AstJit(module, ['a', 'b']) visitor.visit(node) visitor.build_return() print module
Will output the LLVM IR:
; ModuleID = 'ast_jit_module'
define i32 @func_ast_jit(i32 %a, i32 %b) {
entry:
%mul_t = mul i32 3, %b
%add_t = add i32 2, %mul_t
%add_t1 = add i32 %add_t, 165
%add_t2 = add i32 %add_t1, 1
%add_t3 = add i32 %add_t2, 1
%add_t4 = add i32 %add_t3, %a
%sdiv_t = sdiv i32 %add_t4, 2
ret i32 %sdiv_t
}
Now is when the real fun begins, we want to run LLVM optimization passes to optimize our code with an equivalent GCC -O2 optimization level, to do that we create a PassManagerBuilder and a PassManager, the PassManagerBuilder is the component that adds the passes to the PassManager, you can also manually add arbitrary transformations like dead code elimination, function inlining, etc:
pmb = lp.PassManagerBuilder.new() # Optimization level pmb.opt_level = 2 pm = lp.PassManager.new() pmb.populate(pm) # Run the passes into the module pm.run(module) print module
Will output:
; ModuleID = 'ast_jit_module'
define i32 @func_ast_jit(i32 %a, i32 %b) nounwind readnone {
entry:
%mul_t = mul i32 %b, 3
%add_t3 = add i32 %a, 169
%add_t4 = add i32 %add_t3, %mul_t
%sdiv_t = sdiv i32 %add_t4, 2
ret i32 %sdiv_t
}
And here we have the optimized LLVM IR of the Python AST expression. The next step is to JIT that IR into native code and then execute it with some parameters:
ee = ExecutionEngine.new(module) arg_a = GenericValue.int(Type.int(), 100) arg_b = GenericValue.int(Type.int(), 42) retval = ee.run_function(visitor.func_obj, [arg_a, arg_b]) print "Return: %d" % retval.as_int()
Will output:
Return: 197
And that’s it, you have created a AST->LLVM IR converter, optimized the LLVM IR with the transformation passes and then converted it to native code using the LLVM execution engine. I hope you liked =)